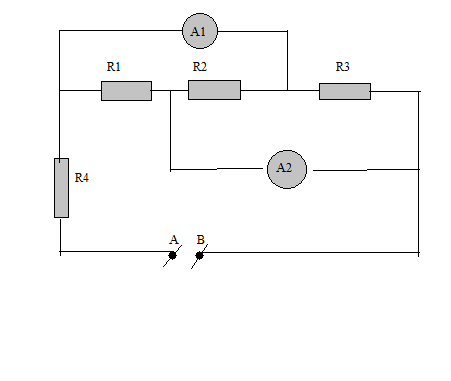
Ta có:
\(R_{23}=R_2+R_3=2+x\left(\Omega\right)\)
\(\Rightarrow\dfrac{1}{R_{2345}}=\dfrac{1}{R_{23}}+\dfrac{1}{R_4}+\dfrac{1}{R_5}=\dfrac{1}{2+x}+\dfrac{1}{6}+\dfrac{1}{4}=\dfrac{5x+22}{12x+24}\)
\(\Rightarrow R_{2345}=\dfrac{12x+24}{5x+22}\)
\(\Rightarrow R_{td}=R_1+R_{2345}=x+\dfrac{12x+24}{5x+22}=\dfrac{5x^2+34x+24}{5x+22}\)
\(\Rightarrow I_{td}=\dfrac{U_{td}}{R_{td}}=\dfrac{35.\left(5x+22\right)}{5x^2+34x+24}\left(1\right)\)
Mà ta có:
\(I_1=I_{2345}=I_{td}=\dfrac{35}{12}\left(2\right)\)
Từ (1) và (2) ta có:
\(\dfrac{35.\left(5x+22\right)}{5x^2+34x+24}=\dfrac{35}{12}\)
\(\Leftrightarrow5x^2-26x-240=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{24}{5}\left(l\right)\\x=10\end{matrix}\right.\)







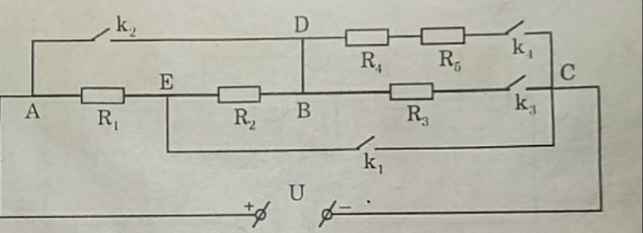


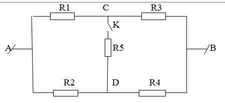

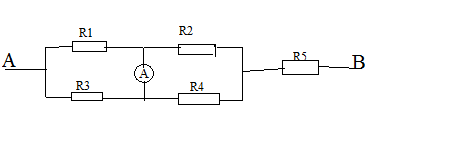

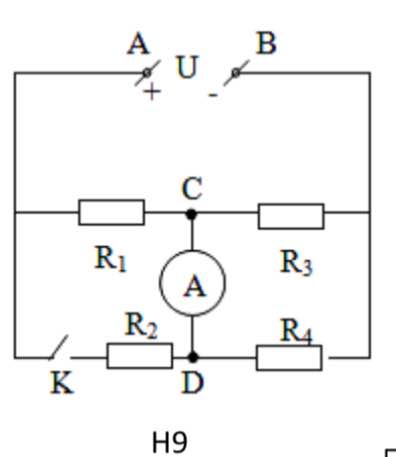
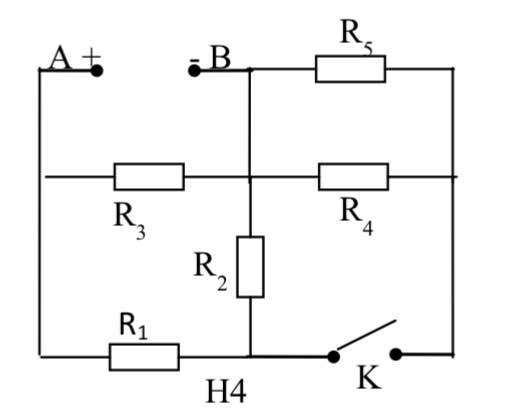 không đổi; điện trở của dây dẫn và khoá không đáng kể.
không đổi; điện trở của dây dẫn và khoá không đáng kể.