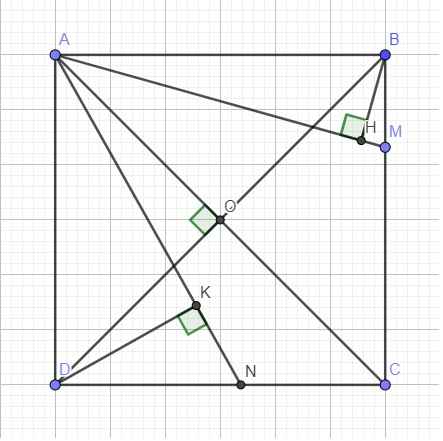
Chi tiết \(BM=DN=\dfrac{a}{3}\) hoàn toàn không cần thiết
a.
Ta có: \(AC\perp BD\) tại O (2 đường chéo hình vuông) \(\Rightarrow O\) thuộc đường tròn đường kính AB
\(AH\perp BH\) (gt) \(\Rightarrow\) H thuộc đường tròn đường kính AB
\(\Rightarrow\) 4 điểm A,B,O,H cùng thuộc đường tròn đường kính AB hay tứ giác ABHO nội tiếp
Hoàn toàn tương tự, 4 điểm ADKO cùng thuộc đường tròn đường kính AD nên tứ giác ADKO nội tiếp
b.
Trong tam giác vuông ABM vuông tại B với đường cao BH, áp dụng hệ thức lượng:
\(AB^2=AH.AM\)
Tương tự, trong tam giác vuông ADN:
\(AD^2=AK.AN\)
Mà \(AB=AD=a\Rightarrow AH.AM=AK.AN\Rightarrow\dfrac{AH}{AN}=\dfrac{AK}{AM}\) (đpcm)