Chương I : Đường thẳng vuông góc. Đường thẳng song song
Các câu hỏi tương tự
Cho góc xoy từ đỉnh A tren tia oy vẽ tia AB ⊥ OX,vẽ BC⊥oy, CD ⊥ Ox ,DE ⊥ Oy (b,dϵOx,C,E ϵ oy)
a) hãy kể tên những cặp dt song song với nhau
b) hình vẽ có nhũng góc nhọn nào bằng nhau
19 tháng 10 2023 lúc 4:29
Cho hình vẽ sau:
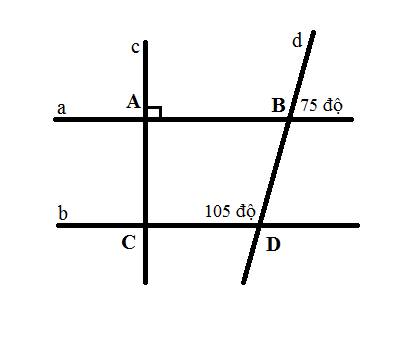
a) Tính số đo góc ABD?
b) Chứng minh a//b
c) Chứng minh \(c\perp b\)
. Cho hình vẽ, biết y/5y/4. Tính x, y
Đọc tiếp
. Cho hình vẽ, biết y/5=y/4. Tính x, y
cho góc nhọn XOY. \(A\in Oy\) vẽ \(AB\perp OX\) ; \(CD\perp OX\);\(BC\perp OY\) ;\(DE\perp OY\) \(\left(a;c;e\in OY\right)\) ; \(\left(B;D\in OX\right)\)
a) kể tên những cặp đường thẳng song song
b) nêu những góc nhọn bằng nhau
Ở miền trong của góc tù AOB vẽ các tia OC, OD sao cho OC ⊥ OA, OD ⊥ OB. Chứng tỏ rằng:
a. \(\widehat{AOD}=\widehat{BOC}\)
b. \(\widehat{AOB}+\widehat{COD}=180^O\)
Cho \(\Delta\)ABC; kẻ AH \(\perp\)BC tại H; AE \(\perp\)AB tại A và AE = AB ( E và C nằm khác phái với AB). Vẽ AF\(\perp\)AC và AF = AC ( F và C nằm khác phía với AC). Kẻ EM và FN cùng \(\perp\)AH tại M và N; EF cắt AH tại I.
CMR: a) EM + BH = HM và FN + CH = HN.
b) I là trung điểm của EF.
3B
cho hai góc kề bù aOb và bOc, biết aOb - bOc= 120. Trong góc aOb vẽ tia Od sao cho aOc = 60. Chứng tỏ \(Ob\perp Od\)
Cho m⊥ n tại K. Vẽ đường thẳng P cắt m, n lần lượt tại A, B tạo ra 1 góc đỉnh B= 110 độ. Tính các góc đỉnh B còn lại.
Cho tam giác ABC, tia phân giác của góc ABC cắt cạnh AC tại H. Từ A kẻ đường thẳng song song vớí BH, cắt CB tại I. Tia phân giác của \(\widehat{ABI}\) cắt AI tại J.
Chứng minh rằng:
a/\(\widehat{AIB}=\widehat{BAI}\)
b/\(BJ\perp AI\)
(Vẽ hình và làm theo yêu cầu)
8 tháng 10 2019 lúc 22:45
Cho tam giác ABC có widehat{A}90^o. Trên nửa mặt phẳng không chứa điểm C bờ là đường thẳng AB, vẽ tia Bx sao cho BA là tia phân giác của widehat{CBx}. Tia này cắt AC tại D. Qua C vẽ đường thẳng vuông góc với AC; đường thẳng này cắt BD tại E. Tia phân giác của góc widehat{CBE}cắt CE tại F. C/m rằng:
a) widehat{BCE}widehat{BEC}
b) Tổng 3 góc trong tam giác ABC bằng 180o
c) BF ⊥ CE
P/s: Không sử dụng kiến thức quá chương 1.
Đọc tiếp
Cho tam giác ABC có \(\widehat{A}=90^o\). Trên nửa mặt phẳng không chứa điểm C bờ là đường thẳng AB, vẽ tia Bx sao cho BA là tia phân giác của \(\widehat{CBx}\). Tia này cắt AC tại D. Qua C vẽ đường thẳng vuông góc với AC; đường thẳng này cắt BD tại E. Tia phân giác của góc \(\widehat{CBE}\)cắt CE tại F. C/m rằng:
a) \(\widehat{BCE}=\widehat{BEC}\)
b) Tổng 3 góc trong tam giác ABC bằng 180o
c) BF ⊥ CE
P/s: Không sử dụng kiến thức quá chương 1.