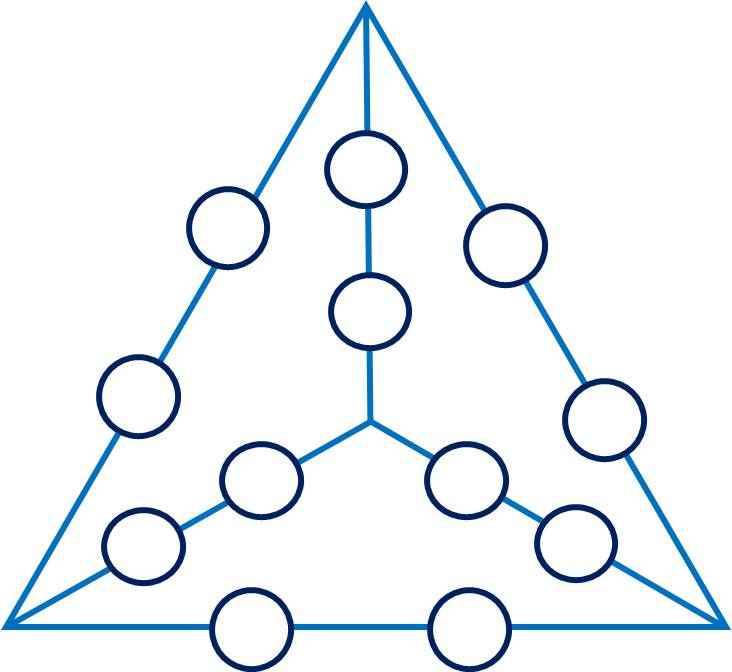
Để giải bài toán này, ta cần xác định giá trị của các ô trống tròn trên mỗi cạnh của tứ diện đều.
Đầu tiên, ta xác định giá trị của mỗi mặt của tứ diện. Vì tứ diện đều có 4 mặt, ta cần tìm tổng của các ô trống tròn trên mỗi mặt. Do đó, tổng mỗi mặt của tứ diện là tổng giá trị của cả 4 ô trống tròn trên mỗi cạnh.
Để điền số tự nhiên từ 1 đến 12 sao cho tổng mỗi mặt bằng nhau, ta có thể sử dụng phương pháp thử và sai. Ta có thể bắt đầu bằng việc điền các số từ 1 đến 12 vào các ô trống tròn trên mỗi cạnh, và sau đó kiểm tra xem tổng mỗi mặt có bằng nhau hay không.
Dưới đây là một cách điền số để tổng mỗi mặt bằng nhau:
6 1 52 4 3 12
Trong trường hợp này, tổng mỗi mặt sẽ là 1 + 2 + 6 + 3 = 12.
Vì vậy, tổng mỗi mặt của tứ diện đều là 12.