Bài 1: Vectơ trong không gian
Các câu hỏi tương tự
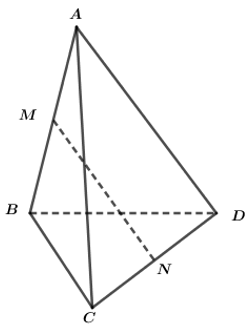
Gọi M và N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn thẳng MN và P là một điểm bất kì trong không gian. Chứng minh :
a) overrightarrow{IA}+overrightarrow{IB}+overrightarrow{IC}+overrightarrow{ID}overrightarrow{0}
b) overrightarrow{PI}dfrac{1}{4}left(overrightarrow{PA}+overrightarrow{PB}+overrightarrow{PC}+overrightarrow{PD}right)
Đọc tiếp
Gọi M và N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn thẳng MN và P là một điểm bất kì trong không gian. Chứng minh :
a) \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\)
b) \(\overrightarrow{PI}=\dfrac{1}{4}\left(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD}\right)\)
Trong không gian cho bốn điểm phân biệt A,B,C,D . gọi M và N lần lượt là trung điểm hai đoạn AB và CD . Đẳng thức nào sau đây không đúng?
A,overrightarrow{MN}frac{1}{2}left(overrightarrow{AC}+overrightarrow{BD}right) B, overrightarrow{MN}frac{1}{2}left(overrightarrow{AD}+overrightarrow{BC}right)
C, overrightarrow{MN}frac{1}{2}left(overrightarrow{AB}+overrightarrow{CD}right) D, overrightarrow{MN}frac{1}{2}left(overrightarrow{AD}-overrightarrow{CB}right)
Đọc tiếp
Trong không gian cho bốn điểm phân biệt A,B,C,D . gọi M và N lần lượt là trung điểm hai đoạn AB và CD . Đẳng thức nào sau đây không đúng?
A,\(\overrightarrow{MN}=\frac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{BD}\right)\) B, \(\overrightarrow{MN}=\frac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{BC}\right)\)
C, \(\overrightarrow{MN}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{CD}\right)\) D, \(\overrightarrow{MN}=\frac{1}{2}\left(\overrightarrow{AD}-\overrightarrow{CB}\right)\)
Cho tứ diện ABCD có M, P lần lượt là trung điểm của AB, CD. Gọi N là điểm thuộc BC sao cho BN3NC, điểm Q thuộc AD sao cho AQxQD. (0 x 1)
a) Tính overrightarrow{MN}, overrightarrow{MP}, overrightarrow{MQ} theo overrightarrow{AB}, overrightarrow{AC}, overrightarrow{AD}.
b) Tìm x để M, N, P, Q đồng phẳng.
Đọc tiếp
Cho tứ diện ABCD có M, P lần lượt là trung điểm của AB, CD. Gọi N là điểm thuộc BC sao cho BN=3NC, điểm Q thuộc AD sao cho AQ=\(x\)QD. (\(0< x< 1\))
a) Tính \(\overrightarrow{MN}\), \(\overrightarrow{MP}\), \(\overrightarrow{MQ}\) theo \(\overrightarrow{AB}\), \(\overrightarrow{AC}\), \(\overrightarrow{AD}\).
b) Tìm \(x\) để M, N, P, Q đồng phẳng.
Cho tam giác ABC. Lấy điểm S nằm ngoài mặt phẳng (ABC). Trên đoạn SA lấy điểm M sao cho \(\overrightarrow{MS}=-2\overrightarrow{MA}\) và trên đoạn BC lấy điểm N sao cho \(\overrightarrow{NB}=-\dfrac{1}{2}\overrightarrow{NC}\). Chứng minh rằng 3 vectơ \(\overrightarrow{AB,}\overrightarrow{MN,}\overrightarrow{SC}\) đồng phẳng ?
Cho tứ diện đều ABCD. Gọi M,N,P lần lượt là trung điểm AB,CB,AD, G là trọng tâm tam giác BCD. Tính góc giữa \(\overrightarrow{MG}\) và \(\overrightarrow{NP}\)
Cho hình hộp ABCD.A'B'C'D' có P và R lần lượt là trung điểm các cạnh AB và A'D'. Gọi P', Q,Q',R' lần lượt là tâm đối xứng của các hình bình hành ABCD, CDD'C', A'B'C'D', ADD'A'
a) Chứng minh rằng \(\overrightarrow{PP'}+\overrightarrow{QQ'}+\overrightarrow{RR'}=\overrightarrow{O}\)
b) Chứng minh hai tam giác PQR và P'Q'R' có trọng tâm trùng nhau
Cho hình tứ diện ABCD. Hãy xác định hai điểm E, F sao cho :
a) \(\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\)
b) \(\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{AD}\)
Cho hình lập phương ABCD.ABCD cạnh a. Gọi O và O theo thứ tự là tâm của hai hình vuông ABCD và ABCD
a) Hãy biểu diễn các vectơ overrightarrow{AO},overrightarrow{AO} theo các vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho
b) Chứng minh rằng :
overrightarrow{AD}+overrightarrow{DC}+overrightarrow{DA}overrightarrow{AB}
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi O và O' theo thứ tự là tâm của hai hình vuông ABCD và A'B'C'D'
a) Hãy biểu diễn các vectơ \(\overrightarrow{AO},\overrightarrow{AO'}\) theo các vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho
b) Chứng minh rằng :
\(\overrightarrow{AD}+\overrightarrow{D'C}+\overrightarrow{D'A'}=\overrightarrow{AB}\)
Cho hình hộp ABCD.ABCD có overrightarrow{AB}overrightarrow{a} overrightarrow{AC}overrightarrow{b} overrightarrow{AA}overrightarrow{c} . Gọi I là trung điểm của BC , K là giao điểm của A I và BD. Phân tích overrightarrow{DK} theo overrightarrow{a},overrightarrow{b},overrightarrow{c}
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có \(\overrightarrow{AB}=\overrightarrow{a}\) \(\overrightarrow{AC}=\overrightarrow{b}\) \(\overrightarrow{AA'}=\overrightarrow{c}\) . Gọi I là trung
điểm của \(B'C'\) , K là giao điểm của A 'I và B'D'. Phân tích \(\overrightarrow{DK}\) theo \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\)