- Đo góc, ta được góc ở đỉnh H của hình thang cân EFGH bằng góc G.
- Các cạnh bên của hình thang cân là EH và FG nên EH = FG (tính chất hình thang cân).
Các đường chéo là EG và FH nên EG = FH (tính chất hình thang cân).
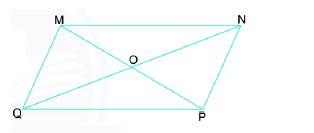
Quan sát hình bình hành bên và cho biết:
- Góc đỉnh M của hình bình hành MNPQ bằng góc nào?
- OM, ON lần lượt bằng những đoạn thẳng nào?
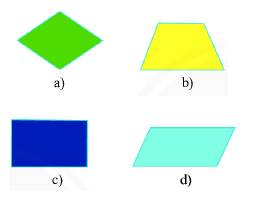
Trong các hình sau đây hình nào là hình chữ nhật, hình bình hành, hình thoi, hình thang cân?
Vẽ hình chữ nhật
Vẽ hình chữ nhật ABCD có AB = 4 cm, AD = 3 cm theo hướng dẫn sau:
- Vẽ đoạn thẳng AB = 4 cm và đoạn thẳng AD = 3 cm vuông góc với nhau.
- Qua B vẽ đường thẳng vuông góc với AB.
- Qua D vẽ đường thẳng vuông góc với AD.
Hai đường thẳng này cắt nhau ở C. ABCD là hình chữ nhật cần vẽ.
Cắt ba hình tam giác đều cạnh 4 cm rồi ghép lại thành một hình thang cân.
Vẽ hình thoi MNPQ biết góc MNP bằng \(60^\circ \) và MN=6 cm.
Người ta có thể thiết kế một mặt bàn hình bình hành bằng cách ghép bốn miếng gỗ hình tam giác đều lại với nhau. Để biết được cách thiết kế như thế nào, hãy cắt 4 hình tam giác đều cạnh 5 cm, rồi ghép thành một hình bình hành.
Gợi ý: Xem hình bên.
Cho hình thang ABCD như Hình 9.
a) Hãy đo rồi so sánh hai cạnh bên BC và AD.
b) Hãy kiểm tra xem AB có song song với CD hay không?
c) AC và BD được gọi là hai đường chéo. Hãy đo rồi so sánh AC và BD.
Cho hình chữ nhật ABCD (Hình 1)
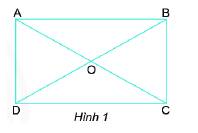
a) Đo rồi so sánh các cạnh và góc của hình chữ nhật.
b) Hãy kiểm tra xem hai cặp cạnh AB và CD, BC và AD có song song với nhau không?
c) AC và BD được gọi là hai đường chéo của hình chữ nhật.
Hãy đo rồi so sánh AC và BD.
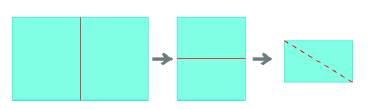
Lấy một tờ giấy hình chữ nhật, gấp đôi hai lần, cắt theo đường nét đứt như hình dưới, rồi trải tờ giấy ra. Hình vừa cắt được là hình gì? Dùng êke để kiểm tra hai đường chéo của hình cắt được có vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường hay không?
