4 tháng 3 2021 lúc 20:58
Bài 6: Trường hợp đồng dạng thứ hai
Các câu hỏi tương tự
Cho ΔABC cân tại A. M là trung điểm của cạnh BC, lấy D và E lần lượt thuộc cạnh AB và AC sao cho \(\widehat{MDB}=\widehat{CME}\)
a) Chứng minh: BM2 = BD.CE
b) Chứng minh: ΔMDE ∼ ΔBDM
1. Cho hình thang vuông ABCD , góc A = góc B = 90 độ , AB = a , cạnh bên CD = AD + BC .
a) Chứng minh : góc CMD = 90 độ , M là trung điểm AB .
b) Chứng minh : AD . BC = a^2/4
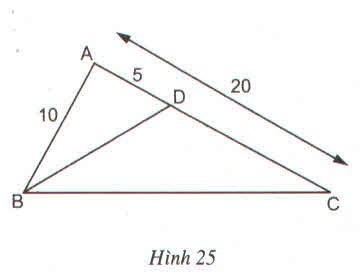
Cho tam giác ABC có AB = 10cm, AC = 20 cm. Trên cạnh AC, đặt đoạn thẳng AD = 5cm (h.25)
Chứng minh \(\widehat{ABD}=\widehat{ACB}\) ?
bài 1 cho tam giác ABC có AB=4,8 , BC=3,6 , AC=6,4 . Trên AB lấy điểm D sao cho AD=3,2 . Trên AC lấy F sao cho AF = 2,4
a, TAM giác ABC đồng dạng tam giác ÀD
b, Tính DF
bài 2 Cho hình thang ABCD ( AB//CD) . Gọi O là trung điểm của 2 đường chéo ,qua O kể dược đường thẳng // 2 đáy của BC ở M , cắt AD ở N
Cmr 1/OM = 1/AB+1/CD
Giúp mình với tối mai đi hc rồi
Hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O và AC = 2.AB
a) Vẽ trung tuyến BE của tam giác ABO. Chứng minh rằng \(\widehat{ABE}=\widehat{ACB}\)
b) Gọi M là trung điểm của cạnh BC, chứng minh rằng EM vuông góc với đường chéo BD
Trên một cạnh của góc xOy \(\left(\widehat{xOy}\ne180^0\right)\), đặt các đoạn thẳng OA = 5cm, OB = 16 cm. Trên cạnh thứ hai của góc đó, đặt các đoạn thẳng OC = 8cm, OD = 10cm
a) Chứng minh hai tam giác OCB và OAD đồng dạng
b) Gọi giao điểm của các cạnh AD và BC là I, chứng minh rằng hai tam giác IAB và ICD có các góc bằng nhau từng đôi một
Hình thang ABCD (AB // CD) có AB = 4cm, CD = 16 cm và BD = 8cm (H.23)
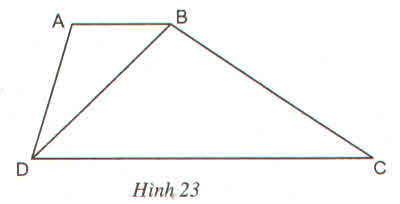
Chứng minh \(\widehat{BAD}=\widehat{DBC}\) và \(BC=2AD\) ?
Cho tam giác ABC có \(\widehat{A}=\widehat{2B}\), AD là tia phân giác góc A .
a)CMR : tam giác CAD đồng dạng với tam giác CBA
b) CMR: \(BC^2=CA^2+AC.AB\)
10 tháng 3 2023 lúc 20:05
a, vẽ tam giác ABC có góc BAC=50 độ ,AB=5cm;AC=7,5 cm
b,lấy trên các cạnh AB,AC lần lượt hai điểm D,E sao cho AD=3cm;AE=2cm.Hai tam giác AED và ABC có đồng dạng với nhau k?Vì sao?