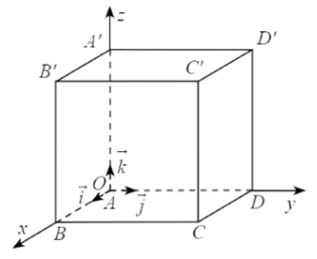
Vi $\overrightarrow{O B}$ và $\vec{i}$ cùng hướng và $O B=5$ nên $\overrightarrow{O B}=5 \vec{i}$.
Tương tự, ta có $\overrightarrow{O D}=5 \vec{j} ; \overrightarrow{O A^{\prime}}=5 \vec{k}$.
Theo quy tắc hình bình hành, ta có: $\overrightarrow{O C}=\overrightarrow{O B}+\overrightarrow{O D}=5 \vec{i}+5 \vec{j}$.
Theo quy tắc hình hộp, ta có: $\overrightarrow{O C^{\prime}}=\overrightarrow{O B}+\overrightarrow{O D}+\overrightarrow{O A^{\prime}}=5 \vec{i}+5 \vec{j}+5 \vec{k}$.
Do đó $B(5 ; 0 ; 0), C(5 ; 5 ; 0), C^{\prime}(5 ; 5 ; 5)$.
Đúng 0
Bình luận (0)


