Question

Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng:

a) \(\overrightarrow{AB}+\overrightarrow{B'C'}+\overrightarrow{DD'}=\overrightarrow{AC'}\);

b) \(\overrightarrow{DB'}+\overrightarrow{D'D}+\overrightarrow{BD'}=\overrightarrow{BB'}\);

c) \(\overrightarrow{AC}+\overrightarrow{BA'}+\overrightarrow{DB}+\overrightarrow{C'D}=\overrightarrow{0}\).

Answer 1

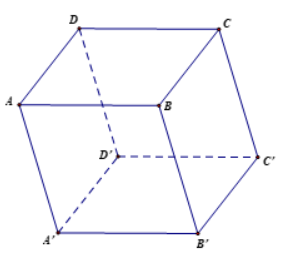
a) \(\overrightarrow {AB}  + \overrightarrow {B'C'}  + \overrightarrow {DD'}  = \overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {AA'}  = \overrightarrow {AC}  + \overrightarrow {AA'}  = \overrightarrow {AC'} \)

b) \(\overrightarrow {DB'}  + \overrightarrow {D'D}  + \overrightarrow {BD'}  = \overrightarrow {D'B'}  + \overrightarrow {BD'}  = \overrightarrow {BB'} \)

c) \(\overrightarrow {AC}  + \overrightarrow {BA'}  + \overrightarrow {DB}  + \overrightarrow {C'D}  = \overrightarrow {A'C'}  + \overrightarrow {DA'}  + \overrightarrow {C'D}  = \overrightarrow {A'D}  + \overrightarrow {DA'}  = \overrightarrow 0 \)