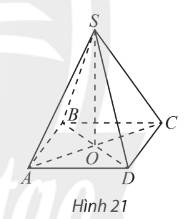
Gọi O là tâm của hình vuông ABCD
=>O là trung điểm chung của AC và BD
a:S.ABCD là hình chóp tứ giác đều nên SO vuông góc (ABCD)
mà \(SO\subset\left(SAC\right)\)
nên \(\left(SAC\right)\perp\left(ABCD\right)\)
b: BD vuông góc SO
BD vuông góc AC
\(SO,AC\subset\left(SAC\right)\)
=>\(BD\perp\left(SAC\right)\)
=>\(\left(SAC\right)\perp\left(SBD\right)\)