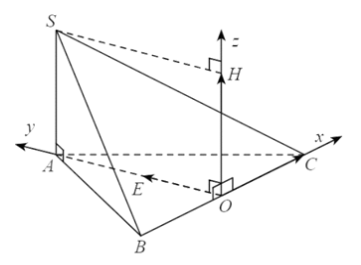
Các vectơ đơn vị trên các trục $\mathrm{Ox}, \mathrm{Oy}$, Oz lần lượt là $\vec{i}=\overrightarrow{O C}, \vec{j}=\overrightarrow{O E}, \vec{k}=\overrightarrow{O H}$ với E là điểm thuộc tia Oy sao cho $\mathrm{OE}=1$ và H là điểm thuộc tia Oz sao cho $\mathrm{OH}=1$.
Vì $\triangle A B C$ đều và $A O \perp B C$ nên $O$ là trung điểm của $B C$.
Mà $B C=2$ nên $O B=O C=1$ và $O A=\sqrt{3}$.
Vì $\overrightarrow{O B}$ và $\vec{i}$ ngược hướng và $\mathrm{OB}=1$ nên $\overrightarrow{O B}=-\vec{i}$. Suy ra $\mathrm{B}(-1 ; 0 ; 0)$.
Vì $\overrightarrow{O C}$ và $\vec{i}$ cùng hướng và $O C=1$ nên $\overrightarrow{O C}=\vec{i}$. Suy ra $C(1 ; 0 ; 0)$.
Vì $\overrightarrow{O A}$ và $\vec{j}$ cùng hướng và $O A=\sqrt{3}$ nên $\overrightarrow{O A}=\sqrt{3} \vec{j}$. Suy ra $A(0 ; \sqrt{3} ; 0)$.
Theo quy tắc hình bình hành, ta có $\overrightarrow{O S}=\overrightarrow{O A}+\overrightarrow{O H}=\sqrt{3} \vec{j}+\vec{k}$. Suy ra $S(0 ; \sqrt{3} ; 1)$.



