\(\begin{array}{l}\left. \begin{array}{l}A \in \left( {ABC} \right)\\B \in \left( {ABC} \right)\end{array} \right\} \Rightarrow AB \subset \left( {ABC} \right)\\\left. \begin{array}{l}B \in \left( {ABC} \right)\\C \in \left( {ABC} \right)\end{array} \right\} \Rightarrow BC \subset \left( {ABC} \right)\\\left. \begin{array}{l}A \in \left( {ABC} \right)\\C \in \left( {ABC} \right)\end{array} \right\} \Rightarrow AC \subset \left( {ABC} \right)\end{array}\)
\(SA \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow SA\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(SB \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow SB\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(SC \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow SC\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(A'B \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow A'B\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(A'C \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow A'C\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(B'A \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow B'A\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(B'C \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow B'C\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(C'A \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow C'A\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(C'B \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow C'B\) cắt mặt phẳng \(\left( {ABC} \right)\).
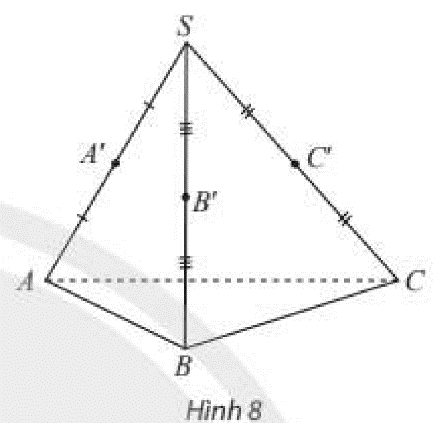
\(A'\) là trung điểm của \(SA\)
\(B'\) là trung điểm của \(SB\)
\( \Rightarrow A'B'\) là đường trung bình của tam giác \(SAB\)
\(\left. \begin{array}{l} \Rightarrow A'B'\parallel AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'B'\parallel \left( {ABC} \right)\)
\(A'\) là trung điểm của \(SA\)
\(C'\) là trung điểm của \(SC\)
\( \Rightarrow A'C'\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow A'C'\parallel AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'C'\parallel \left( {ABC} \right)\)
\(B'\) là trung điểm của \(SB\)
\(C'\) là trung điểm của \(SC\)
\( \Rightarrow B'C'\) là đường trung bình của tam giác \(SBC\)
\(\left. \begin{array}{l} \Rightarrow B'C'\parallel BC\\BC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow B'C'\parallel \left( {ABC} \right)\)