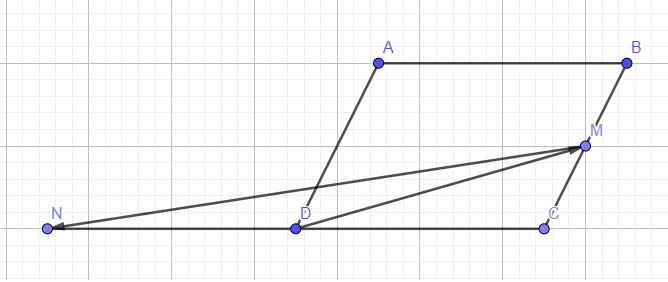
\(\overrightarrow{NC}=2\overrightarrow{ND}=2\overrightarrow{NC}+2\overrightarrow{CD}\Rightarrow\overrightarrow{NC}=2\overrightarrow{DC}\Rightarrow\overrightarrow{CN}=2\overrightarrow{CD}\)
a.
\(\overrightarrow{DM}=\overrightarrow{DC}+\overrightarrow{CM}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{CB}=\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\)
\(\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\dfrac{1}{2}\overrightarrow{BC}+2\overrightarrow{CD}=-2\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
b.
\(\left\{{}\begin{matrix}\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\\\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}=-\overrightarrow{AB}+\overrightarrow{AD}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{BD}\\\overrightarrow{AD}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BD}\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MN}=-2\left(\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{BD}\right)+\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BD}\right)=-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{5}{4}\overrightarrow{BD}\)