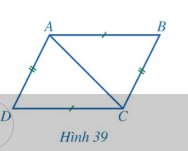
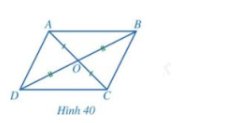
Cho hình bình hành ABCD (Hình 37).
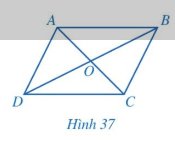
a) Hai tam giác ABD và CDB có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: AB và CD; DA và BC.
b) So sánh các cặp góc: \(\widehat {DAB}\) và \(\widehat {BCD}\); \(\widehat {ABC}\) và \(\widehat {CDA}\).
c) Hai tam giác OAB và OCD có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: OA và OC; OB và OD.
a) Xét tam giác ABD và tam giác CDB có:
\(\widehat {ABD} = \widehat {CDB}\) ( vì AB //CD)
BD chung
\(\widehat {ADB} = \widehat {CBD}\) (vì AD // BC)
Suy ra: \(\Delta ABD = \Delta CDB\)(g - c - g)
Suy ra: AB = CD, DA = BC.
b) Vì \(\Delta AB{\rm{D}} = \Delta C{\rm{D}}B\) (g - c - g) suy ra: \(\widehat {DAB}\) = \(\widehat {BCD}\)
Xét tam giác ABC và tam giác CDA có:
AB = CD (cmt)
Cạnh AC chung
BC = AD (cmt)
\(\Delta ABC = \Delta CDA (c - c - c) \Rightarrow \widehat {ABC} = \widehat {CDA}\) (2 góc tương ứng)
c) Xét tam giác OAB và OCD có:
\(\begin{array}{l}\widehat {OAB} = \widehat {OCD} (cmt)\\AB = CD (cmt)\\\widehat {OBA} = \widehat {ODC} (cmt)\end{array}\)
Suy ra: \(\Delta OAB = \Delta OC{\rm{D}}\) (g - c - g) suy ra: OA = OC; OB = OD (các cạnh tương ứng)