Question

Cho hình bình hành ABCD. Dựng các tam giác đều ADE,DCF về phía ngoài hình bình hành. chứng minh BEF đều

Answer 1

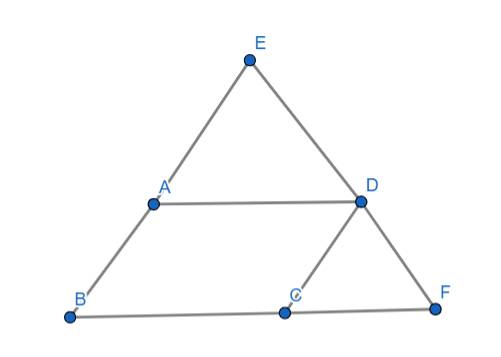
Đặt độ dài cạnh AD là a, độ dài cạnh AB là b

Ta có: ABCD là hình bình hành nên:

\(AB=CD=b\) (hai cạnh bên) 

Mà: DCF là tam giác đều nên: 

\(CD=CF=DF=b\) (ba cạnh tam giác đều) 

Và: \(AD=BC=a\)

\(\Rightarrow BF=BC+CF=a+b\) (1)

Và: ΔADE là tam giác đều nên:

\(AD=DE=AE=a\) 

\(\Rightarrow BE=AB+AE=a+b\) (2) 

\(\Rightarrow EF=DE+DF=a+b\) (3) 

Từ (1) và (2) và (3)

\(\Rightarrow BE=BF=EF=a+b\)

Vậy ΔBEF là tam giác đều (đpcm)