Question

Cho hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O thỏa mãn \(\widehat {OAB} = \widehat {O{\rm{D}}C}\). Chứng minh ABCD là hình chữ nhật.

Answer 1

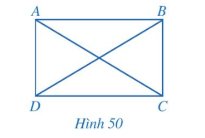
Do ABCD là hình bình hành suy ra AB = CD và AB // CD nên \(\widehat{ABO}=\widehat{ODC}\) (hai góc so le trong\)

Mà \(\widehat {OAB} = \widehat {O{\rm{D}}C}\) nên \(\widehat{ABO}=\widehat{OAB}\) suy ra tam giác AOB cân tại O.

Vì tam giác AOB cân tại O nên OA = OB.

Mà hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường nên AC = BD.

Suy ra ABCD có hai đường chéo AC = BD nên ABCD là hình chữ nhật.