Ôn tập Hệ thức lượng trong tam giác vuông
Các câu hỏi tương tự
1. Cho tam giác ABC vuông tại A có AB 9 cm , BC 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,2. Cho tam giác ABC vuông tại A có AC 5 cm , AB 4 cm . Tính : a ) Cạnh huyền BC . b ) Hình chiếu của AB và AC trên cạnh huyền . c ) Đường cao AH . 3. Cho tam giác ABC vuông tại A có BC 40 cm , AC 36 cm . Tính AB , BH , CH và AH ,4. Cho tam giác ABC vuông tại A có BC 24 cm . Tính AB , AC , cho biết 2 AB -AC .5. Cho tam giác ABC vuông tại A có AH là đường cao . BH 10 cm ,...
Đọc tiếp
1. Cho tam giác ABC vuông tại A có AB = 9 cm , BC = 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,
2. Cho tam giác ABC vuông tại A có AC = 5 cm , AB = 4 cm . Tính : a ) Cạnh huyền BC . b ) Hình chiếu của AB và AC trên cạnh huyền . c ) Đường cao AH .
3. Cho tam giác ABC vuông tại A có BC = 40 cm , AC = 36 cm . Tính AB , BH , CH và AH ,
4. Cho tam giác ABC vuông tại A có BC = 24 cm . Tính AB , AC , cho biết 2 AB = -AC .
5. Cho tam giác ABC vuông tại A có AH là đường cao . BH = 10 cm , CH = 42 cm . Tính BC , AH , AB và AC ,
6. Cho đường tròn tâm O bán kính R = 10 cm . A , B là hai điểm trên đường tròn ( O ) và I là trung điểm của đoạn thẳng AB . a ) Tính AB nếu OI = 7 cm . b ) Tính OI nếu AB = 14 cm .
Xem hình 37.
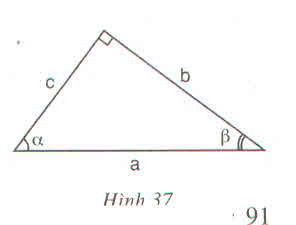
a) Hãy viết công thức tính các góc vuông b và c theo cạnh huyền a và tỉ số lượng giác của các góc \(\alpha,\beta\)
b) Hãy viết công thức tính mỗi cạnh góc vuông theo cạnh góc vuông kia và tỉ số lượng giác của các góc \(\alpha,\beta\)
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC
a) Tính độ dài đoạn thẳng DE
b) Các đường thẳng vuông góc với DE tại D và tại E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH
c) Tính diện tích tứ giác DENM
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC
a) Tính độ dài đoạn thẳng DE
b) Các đường thẳng vuông góc với DE tại D và tại E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH
c) Tính diện tích tứ giác DENM
bài 99 gọi a,b.c là các cạnh của 1 tam giác vuông ,h là đường cao ứng với cạnh huyền a. chứng minh rằng tam giác có các cạnh a+h ; b+c và h cũng là 1 tam giác vuông
helppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppp
cho ΔABC vuông tại A, đường cao AH.Gọi E,F lần lượt là hình chiếu của H trên AB,AC.1)Cho AB9cm,BH5,4cm.Tính các cạnh AC,BC,AH,FE.Tính các góc ABC,HAC(làm tròn đến độ)2) Tính diện tích tứ giác AEHF, tam giác AFE3) Kẻ đường phân giác AD,từ D kẻ DPperpAB,DQperpAC.Tính BD,CD,AD, chu vi và diện tích AQDP4) chứng minh rằng:a) AE.ABAF.ACHB.HC b)BCAB.cosB+AC.cosCc)tanB.sinBHC/AB d)cosC.sinBHC/BC5)Chứng minh rằng: 1/EF2 1/AB2 + 1/AC2 6) Chứng minh rằng: EA.EB+FA.FCHB.HC
Đọc tiếp
cho ΔABC vuông tại A, đường cao AH.Gọi E,F lần lượt là hình chiếu của H trên AB,AC.
1)Cho AB=9cm,BH=5,4cm.Tính các cạnh AC,BC,AH,FE.Tính các góc ABC,HAC(làm tròn đến độ)
2) Tính diện tích tứ giác AEHF, tam giác AFE
3) Kẻ đường phân giác AD,từ D kẻ DP\(\perp\)AB,DQ\(\perp\)AC.Tính BD,CD,AD, chu vi và diện tích AQDP
4) chứng minh rằng:
a) AE.AB=AF.AC=HB.HC b)BC=AB.cosB+AC.cosC
c)tanB.sinB=HC/AB d)cosC.sinB=HC/BC
5)Chứng minh rằng: 1/EF2 =1/AB2 + 1/AC2
6) Chứng minh rằng: EA.EB+FA.FC=HB.HC
cho ΔABC vuông tại A, đường cao AH.Gọi E,F lần lượt là hình chiếu của H trên AB,AC.1)Cho AB9cm,BH5,4cm.Tính các cạnh AC,BC,AH,FE.Tính các góc ABC,HAC(làm tròn đến độ)2) Tính diện tích tứ giác AEHF, tam giác AFE3) Kẻ đường phân giác AD,từ D kẻ DP⊥⊥AB,DQ⊥⊥AC.Tính BD,CD,AD, chu vi và diện tích AQDP4) chứng minh rằng:a) AE.ABAF.ACHB.HC b)BCAB.cosB+AC.cosCc)tanB.sinBHC/AB d)cosC.sinBHC/BC5)Chứng minh rằng: 1/EF2 1/AB2 + 1/AC2 6) Chứng minh rằng: EA.EB+FA.FCHB.HC
Đọc tiếp
cho ΔABC vuông tại A, đường cao AH.Gọi E,F lần lượt là hình chiếu của H trên AB,AC.
1)Cho AB=9cm,BH=5,4cm.Tính các cạnh AC,BC,AH,FE.Tính các góc ABC,HAC(làm tròn đến độ)
2) Tính diện tích tứ giác AEHF, tam giác AFE
3) Kẻ đường phân giác AD,từ D kẻ DP⊥⊥AB,DQ⊥⊥AC.Tính BD,CD,AD, chu vi và diện tích AQDP
4) chứng minh rằng:
a) AE.AB=AF.AC=HB.HC b)BC=AB.cosB+AC.cosC
c)tanB.sinB=HC/AB d)cosC.sinB=HC/BC
5)Chứng minh rằng: 1/EF2 =1/AB2 + 1/AC2
6) Chứng minh rằng: EA.EB+FA.FC=HB.HC
cho tam giác vuông có các độ dài các góc vuông là 6cm và 8cm.đọ dài cạnh huyền là
Cho tam giác ABC vuông tại A, đường cao AH. Biết BC=8cm, BH=2cm. a) Tính độ dài các đoạn thẳng AB, AC, AH b) Trên cạnh AC lấy điểm K (K khác A, K khác C), gọi D là hình chiếu của A trên BK. Chứng minh BD.BK=BH.BC từ đó suy ra AB = BC. sin góc BDH
Cho tam giác ABC vuông tại A có AH là đường cao chia cạnh huyền BC thành hai đoạn BH=4cm; HC = 6cm
b) gọi M là chung điểm của AC. Tính số đo góc AMB( làm tròn đến độ)
c)kẻ AK vuông góc với BM (K thuộc BM) . Chứng minh BK.BM=BH.BC