Question

Cho hình 107, trong đó ABCD là hình vuông. Chứng minh rằng tứ giác EFGH là hình vuông ?

Answer 1

Bài giải:

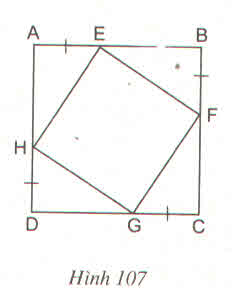
Các tam giác vuông AEH, BFC, CGF, DHG có:

AE = BF = CG = DH (gt)

Suy ra AH = BE = CF = DG

Nên ∆AEH = ∆BFE = ∆CGF = ∆DHG (c.g.c)

Do đó HE = EF = FG = GH (1)

và =

Ta có = 180⁰ - ( + ) = 180⁰ - ( + )

= 180⁰ - 90⁰ = 90⁰ (2)

^{Từ (1) và (2) ta được EFGH là hình vuông}

Answer 2

Các tam giác vuông AEH, BFC, CGF, DHG có:

AE = BF = CG = DH (gt)

Suy ra AH = BE = CF = DG

Nên ∆AEH = ∆BFE = ∆CGF = ∆DHG (c.g.c)

Do đó HE = EF = FG = GH (1)

và ˆEHAEHA^ = ˆFEBFEB^

Ta có ˆHEFHEF^ = 1800 - (ˆHEAHEA^ + ˆFEBFEB^) = 1800 - (ˆHEAHEA^ + ˆEHAEHA^)

= 1800 - 900 = 900 (2)

Từ (1) và (2) ta được EFGH là hình vuông.

Answer 3

Các tam giác vuông AEH, BFC, CGF, DHG có:

AE = BF = CG = DH (gt)

Suy ra AH = BE = CF = DG

Nên ∆AEH = ∆BFE = ∆CGF = ∆DHG (c.g.c)

Do đó HE = EF = FG = GH (1)

và $\widehat{EHA}$ = $\widehat{FEB}$

Ta có $\widehat{HEF}$ = 180⁰ - ($\widehat{HEA}$ + $\widehat{FEB}$) = 180⁰ - ($\widehat{HEA}$ + $\widehat{EHA}$)

= 180⁰ - 90⁰ = 90⁰ (2)

^{Từ (1) và (2) ta được EFGH là hình vuông.}

Answer 4