Xét tam giác A’B’C’ và tam giác ABC có:
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) và \(\widehat {A'} = \widehat A = 90^\circ \)
\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\) (c-g-c)
Xét tam giác A’B’C’ và tam giác ABC có:
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) và \(\widehat {A'} = \widehat A = 90^\circ \)
\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\) (c-g-c)
Cho \(\Delta ABC \backsim \Delta MNP\).
a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh \(\Delta ABD \backsim \Delta MNQ\).
b) Gọi G và K lần lượt là trọng tâm của hai tam giác ABC và MNP. Chứng minh \(\Delta ABG \backsim \Delta MNK\).
Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ sao cho \(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\). Chứng minh \(\widehat B = \widehat {B'}\).
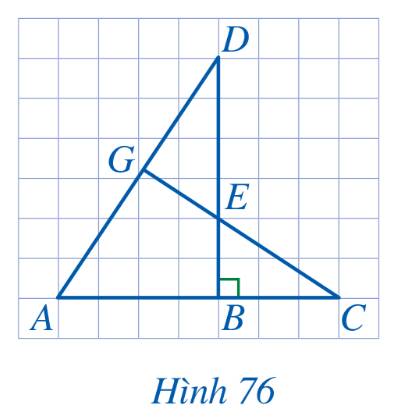
Cho Hình 76, biết \(AB = 4,\,\,BC = 3,\,\,BE = 2,\,\,BD = 6\). Chứng minh:
a) \(\Delta ABD \backsim \Delta EBC\)
b) \(\widehat {DAB} = \widehat {DEG}\)
c) Tam giác DGE vuông
Cho hai tam giác ABC và A’B’C’ thỏa mãn \(AB = 2,AC = 3,A'B' = 6,A'C' = 9\) và \(\widehat A = \widehat {A'}\). Chứng minh \(\widehat B = \widehat {B'},\,\,\widehat C = \widehat {C'}\).
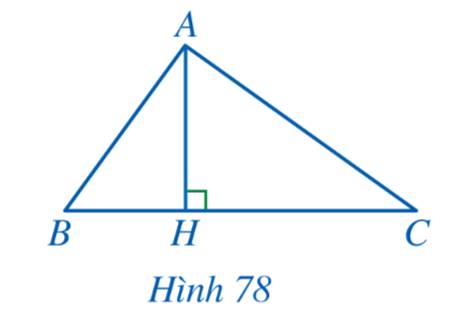
Cho Hình78, biết \(A{H^2} = BH.CH\). Chứng minh:
a) \(\Delta HAB \backsim \Delta HCA\)
b) Tam giác ABC vuông tại A.
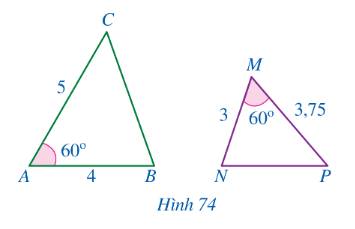
Cho Hình 74.
a) Chứng minh \(\Delta ABC \backsim \Delta MNP\)
b) Góc nào của tam giác MNP bằng góc B?
c) Góc nào của tam giác ABC bằng góc P?
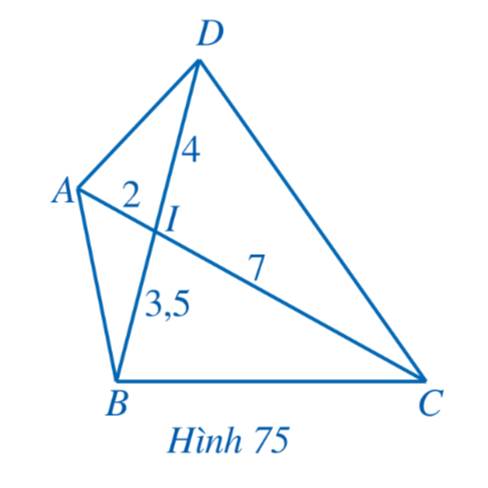
Cho Hình 75, chứng minh:
a) \(\Delta IAB \backsim \Delta IDC\)
b) \(\Delta IAD \backsim \Delta IBC\)
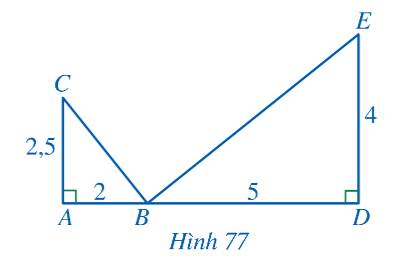
Cho Hình 77, chứng minh
a) \(\widehat {ABC} = \widehat {BED}\)
b) \(BC \bot BE\)
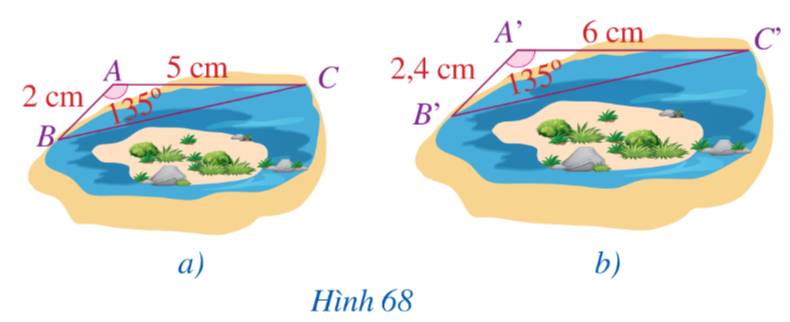
Quan sát hình 68 và so sánh:
a) Các tỉ số \(\frac{{A'B'}}{{AB}}\) và \(\frac{{A'C'}}{{AC}}\)
b) Các góc \(\widehat A\) và \(\widehat {A'}\)