Question

Cho hai góc kề bù và Biết
Khi đó ....

Answer 1

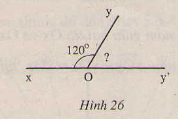
Ta có:

\(\widehat{AOB}+\widehat{BOC}=180^0\)

Mà \(\widehat{AOB}=2\widehat{BOC}\)

\(\Rightarrow2\widehat{BOC}+\widehat{BOC}=180^0\)

\(\Leftrightarrow3\widehat{BOC}=180^0\)

\(\Rightarrow\widehat{BOC}=\frac{180^0}{3}\)

\(\Rightarrow\widehat{BOC}=60^0\)

Vậy \(\widehat{BOC}\) bằng \(180^0\).

Answer 2

Ta có : \(\widehat{AOB}+\widehat{BOC}\) = \(180^o\)( vì kề bù )

Mà \(\widehat{AOB}=2.\widehat{BOC}\)

=> \(2.B\widehat{OC}+\widehat{BOC}=180^o\)

\(\Leftrightarrow3.\widehat{BOC}=180^o\)

\(\Leftrightarrow\widehat{BOC}=180^o:3\)

\(\Leftrightarrow\widehat{BOC}=60^o\)

Vậy khi đó \(\widehat{BOC}=60^o\)