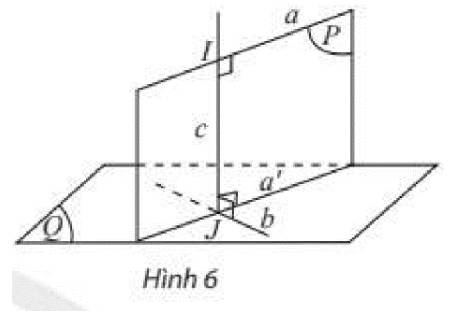
Cho hai đường thẳng chéo nhau \(a\) và \(b\). Gọi \(\left( Q \right)\) là mặt phẳng chứa \(b\) và song song với \(a\). Gọi \(\left( P \right)\) là mặt phẳng chứa đường thẳng \(a\), vuông góc với \(\left( Q \right)\) và cắt \(b\) tại điểm \(J\). Trong \(\left( P \right)\), gọi \(c\) là đường thẳng đi qua \(J\), vuông góc với \(a\) và cắt \(a\) tại điểm \(I\).
Đường thẳng \(IJ\) có vuông góc với \(b\) không? Giải thích.
Gọi (R) là mặt phẳng chứa a và (R)//(Q)
(Q)//(R)
\(\left(P\right)\cap\left(Q\right)=a'\)
\(\left(P\right)\cap\left(R\right)=a\)
Do đó: a//a'
mà IJ vuông góc a
nên JI vuông góc a'
\(\left(P\right)\perp\left(Q\right)\)
\(\left(P\right)\cap\left(Q\right)=a'\)
\(JI\perp a\)
Do đó: JI vuông góc (Q)
=>IJ vuông góc b
tham khảo:
Gọi (R) là mặt phẳng chứa a song song với (Q).
(P) cắt hai mặt phẳng song song tại a và a' nên a//a'
Trong mặt phẳng (P), IJ⊥a,a//a′ nên IJ⊥a′
Ta có: (P)⊥(Q), (P) cắt (Q) tại a', IJ⊥a′ nên IJ⊥(P)
Suy ra IJ⊥b









