Chương II - Đường tròn
Các câu hỏi tương tự
Cho nửa đường tròn tâm O đường kính AB=2R. Gọi C là 1 điểm tùy ý trên nửa đường tròn (O) sao cho AC>BC (A, B khác C). Qua O kẻ đường thẳng vuông góc với AB cắt dây AC tại D. a) Chứng minh tứ giác BCDO nội tiếp b) Chứng minh AD.AC=AO.AB c) Vẽ tiếp tuyến tại C của đường tròn (O). Từ D vẽ đường thẳng song song với AB cắt tiếp tuyến này tại E. Chứng minh AD//OE.
Cho đường tròn (O) đường kính AB cố định. Từ điểm C bất kỳ trên đoạn OA vẽ dây MN vuông góc với AB. Lấy điểm D thuộc cung AM nhỏ; BD cắt MN tại E; AD cắt tia NM tại F. a) Chứng minh : tứ giác ADEC nội tiếp. b) Chứng minh: CA.CB CE.CF c) Tia AE cắt đường tròn ngoại tiếp tam giác DEF tại điểm I. Chứng minh I nằm trên đường tròn O. d) Xác định vị trí của điểm C trên OA sao cho chu vi tam giác OCN lớn nhất
Đọc tiếp
Cho đường tròn (O) đường kính AB cố định. Từ điểm C bất kỳ trên đoạn OA vẽ dây MN vuông góc với AB. Lấy điểm D thuộc cung AM nhỏ; BD cắt MN tại E; AD cắt tia NM tại F. a) Chứng minh : tứ giác ADEC nội tiếp. b) Chứng minh: CA.CB = CE.CF c) Tia AE cắt đường tròn ngoại tiếp tam giác DEF tại điểm I. Chứng minh I nằm trên đường tròn O. d) Xác định vị trí của điểm C trên OA sao cho chu vi tam giác OCN lớn nhất
Cho (O) có đường kính AB=2R, C là trung điểm của OA và dây MN vuông góc với OA tại C. Gọi E là điểm tùy ý trên cung nhỏ BM, H là giao điểm của AE và MN CMR: MA là tiếp tuyến của đường tròn ngoại tiếp tam giác AMH.
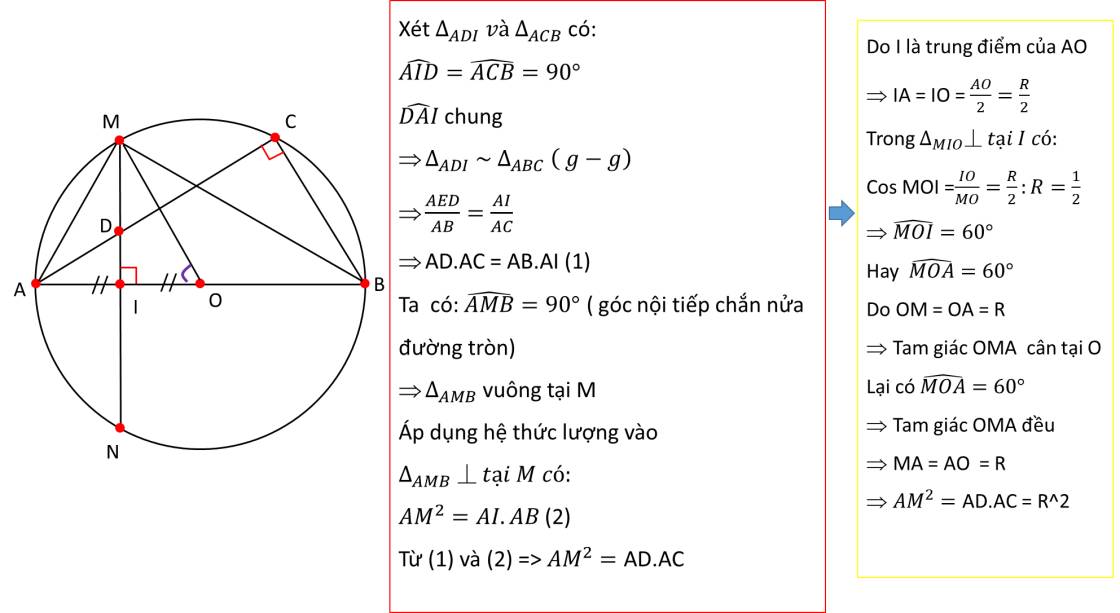
Cho đường tròn (O;R) đường kính AB. Gọi I là dây cung của OA. Vẽ dây CD vuông góc với OA tại I. Lấy điểm E tùy ý trên cung nhỏ BC (E khác B và C). Gọi K là giao điểm của AE và BC. Kẻ KH vuông góc AB (H thuộc AB)1) Chứng minh rằng BEHK là tứ giác nội tiếp.2) Chứng minh rằng HK là tia phân giác của EHC và ba điểm E, H, D thẳng hàng.3) Tìm vị trí của điểm E trên cung nhỏ BC sao cho chu vi ACEB lớn nhất.
Đọc tiếp
Cho đường tròn (O;R) đường kính AB. Gọi I là dây cung của OA. Vẽ dây CD vuông góc với OA tại I. Lấy điểm E tùy ý trên cung nhỏ BC (E khác B và C). Gọi K là giao điểm của AE và BC. Kẻ KH vuông góc AB (H thuộc AB)
1) Chứng minh rằng BEHK là tứ giác nội tiếp.
2) Chứng minh rằng HK là tia phân giác của EHC và ba điểm E, H, D thẳng hàng.
3) Tìm vị trí của điểm E trên cung nhỏ BC sao cho chu vi ACEB lớn nhất.
Cho nửa đường tròn tâm O đường kính AB=2R, I là trung điểm AO.Dựng đường thẳng d đi qua I vuông góc với AB cắt đường tròn tại K. Lấy 1 điểm C thuộc IK, AC cắt nửa đường tròn tại M. Tiếp tuyến qua M cắt d tại N, BM cắt d tại D.
a) Chứng minh N là trung điểm CD
b) Tính CD khi C là trung điểm của IK
Cần Ý B
Từ điểm A nằm ngoài (O;R) vẽ các tiếp tuyến AM,AN (M,N là 2 điểm). MN cắt AO tại H. a) chứng minh 4 điểm A,M,O,N cứng thuộc đường tròn. Xác định tâm I và bán kính của đường tròn. b) chứng minh OA vuông góc MN tại H là trung điểm của MN. c) chứng minh AM2=AH.AO=OA2-R2. d) vẽ đường kính MD của (O). Chứng minh ND song song OA và 2OH=ND
Cho nửa đường tròn (O;R), đường kính AB, H thuộc OA. Qua H kẻ đường thẳng vuông góc với AB cắt nửa đuòng tròn (O) tại M. Gọi I là trung điểm MH, tia AI cắt nửa đường tròn (O) tại C, tia BC cắt tia HM tại D
1. Chứng minh 4 diểm: B, H, I, C thuộc một đuòng tròn, xác đinh tâm của đường tròn đó.
cho đường tròn tâm O bán kính r và 1 điểm A sao cho OA bằng 2R, vẽ các tiếp tuyến AB và Ac với đường tròn kẻ đường kính kính BD a) chứng minh DC//OA b) cho đường trung trực của BD cắt AC và CD tại S và E. Cm OCEA là hình thang cân c) gọi I là giao điểm OA với (O). Cm SI à tiếp tuyến (O) d) tia SI cắt AB tại K. Cm tứ giác AKOS là hình thoi
Bài 12. Cho nửa đường tròn (O) đường kính AB 2R và dây cung AC R. Gọi K là trung điểm của dây cung CB, qua B dựng tiếp tuyến Bx với (O) cắt tia OK tại D.a) Chứng minh rằng : DeltaABC vuông. b) Chứng minh rằng : DC là tiếp tuyến của đường tròn (O). c) Tia OD cắt (O) tại M. Chứng minh rằng : Tứ giác OBMC là hình thoi . d) Vẽ CH vuông góc với AB tại H và gọi I là trung điểm của cạnh CH. Tiếp...
Đọc tiếp
Bài 12. Cho nửa đường tròn (O) đường kính AB = 2R và dây cung AC = R. Gọi K là trung điểm của dây cung CB, qua B dựng tiếp tuyến Bx với (O) cắt tia OK tại D.
a) Chứng minh rằng : \(\Delta\)ABC vuông.
b) Chứng minh rằng : DC là tiếp tuyến của đường tròn (O).
c) Tia OD cắt (O) tại M. Chứng minh rằng : Tứ giác OBMC là hình thoi .
d) Vẽ CH vuông góc với AB tại H và gọi I là trung điểm của cạnh CH. Tiếp tuyến tại A của đường tròn (O) cắt tia BI tại E. Chứng minh rằng ba điểm E, C, D thẳng hàng.