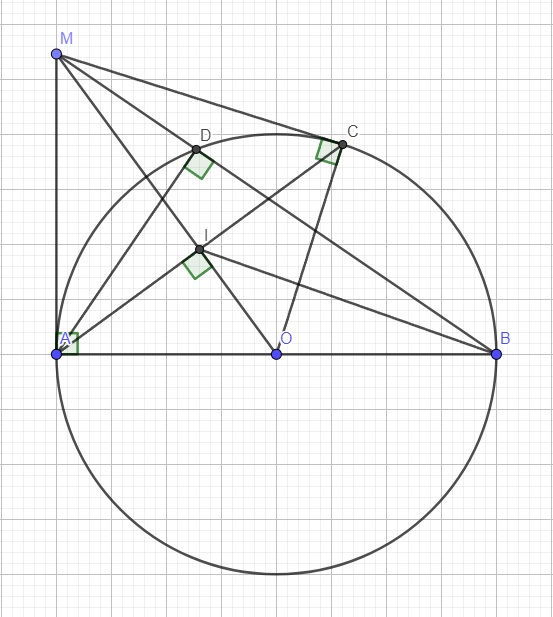
cho đường tròn tâm O ,đường kính AB .Trên tia tiếp tuyến Ax của đường trong (O) lấy điểm M(M khác A), kể tiếp tuyến MC với đường tròn (O)(C là tiếp điểm).(yêu cầu vẽ hình)
a)Chứng minh bốn điểm O,A,M,C cùng thuộc 1 đường tròn
b)chứng minh OM\(\perp\)AC tại I
c)Tia BM cắt đường tròn (O) tại D (D ≠ B).chứng minh :MA2 =MI.MO=MD.MB
d)chứng minh:góc OIB = góc OBM\(\)
a.
Do AM là tiếp tuyến của (O) \(\Rightarrow AM\perp OA\Rightarrow\widehat{OAM}=90^0\)
\(\Rightarrow\) 3 điểm O, A, M cùng thuộc đường tròn đường kính OM (1)
Tương tự, do MC là tiếp tuyến của (O) \(\Rightarrow\widehat{OCM}=90^0\)
\(\Rightarrow\) 3 điểm O, C, M cùng thuộc đường tròn đường kính OM (2)
(1);(2) \(\Rightarrow\) 4 điểm O, A, M, C cùng thuộc đường tròn đường kính OM
b.
Do M là giao điểm 2 tiếp tuyến của (O) tại A và C \(\Rightarrow MA=MC\) (t/c hai tiếp tuyến cắt nhau)
Lại có \(OA=OC=R\)
\(\Rightarrow OM\) là trung trực của AC
\(\Rightarrow OM\perp AC\) tại I
c.
Do AB là đường kính và D thuộc đường tròn \(\Rightarrow\widehat{ADB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{ADB}=90^0\) hay \(AD\perp BM\)
Áp dụng hệ thức lượng trong tam giác vuông BAM với đường cao AD:
\(AM^2=MD.MB\) (3)
Theo c/m câu b ta có \(AI\perp MO\), áp dụng hệ thức lượng trong tam giác vuông OAM với đường cao AI:
\(AM^2=MI.MO\) (4)
(3);(4) \(\Rightarrow MA^2=MI.MO=MD.MB\)
d.
Áp dụng hệ thức lượng trong tam giác vuông OAM với đường cao AI:
\(OA^2=OI.OM\)
Mà \(OA=OB=R\Rightarrow OB^2=OI.OM\Rightarrow\dfrac{OI}{OB}=\dfrac{OB}{OM}\)
Xét hai tam giác BOI và MOB có:
\(\left\{{}\begin{matrix}\dfrac{OI}{OB}=\dfrac{OB}{OM}\left(cmt\right)\\\widehat{MOB}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BOI\sim\Delta MOB\left(c.g.c\right)\)
\(\Rightarrow\widehat{OIB}=\widehat{OBM}\)