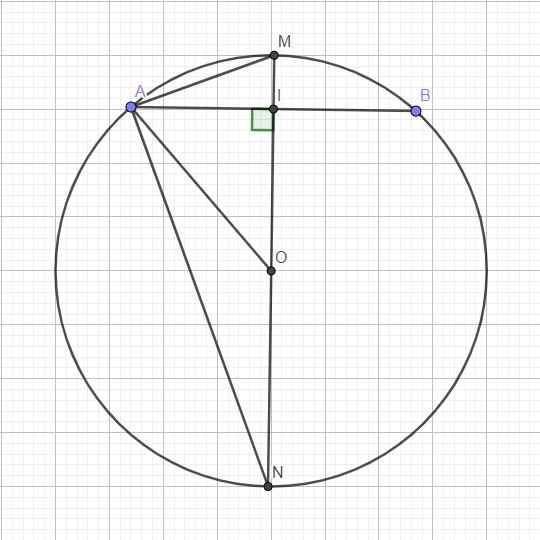
Do I là trung điểm AB \(\Rightarrow OI\perp AB\)
\(AI=\dfrac{1}{2}AB=3\)
Trong tam giác vuông OAI, áp dụng Pitago:
\(OI=\sqrt{OA^2-AI^2}=\sqrt{R^2-AI^2}=4\)
\(\Rightarrow IM=OM-OI=R-OI=1\)
\(\Rightarrow AM=\sqrt{AI^2+IM^2}=\sqrt{10}\left(cm\right)\)
b.
Vẫn như trên, ta có: \(AI=\dfrac{1}{2}AB=6\)
Do MN là đường kính \(\Rightarrow\Delta MAN\) vuông tại A
Áp dụng hệ thức lượng trong tam giác vuông MAN với đường cao AI:
\(\dfrac{1}{AI^2}=\dfrac{1}{AN^2}+\dfrac{1}{AM^2}\Rightarrow\dfrac{1}{6^2}=\dfrac{1}{10^2}+\dfrac{1}{AM^2}\Rightarrow AM=\dfrac{15}{2}\)
Áp dụng hệ thức lượng:
\(AI.MN=AN.AM\Leftrightarrow MN=\dfrac{AM.AN}{AI}=\dfrac{25}{2}\)
\(\Rightarrow R=\dfrac{MN}{2}=\dfrac{25}{4}\left(cm\right)\)