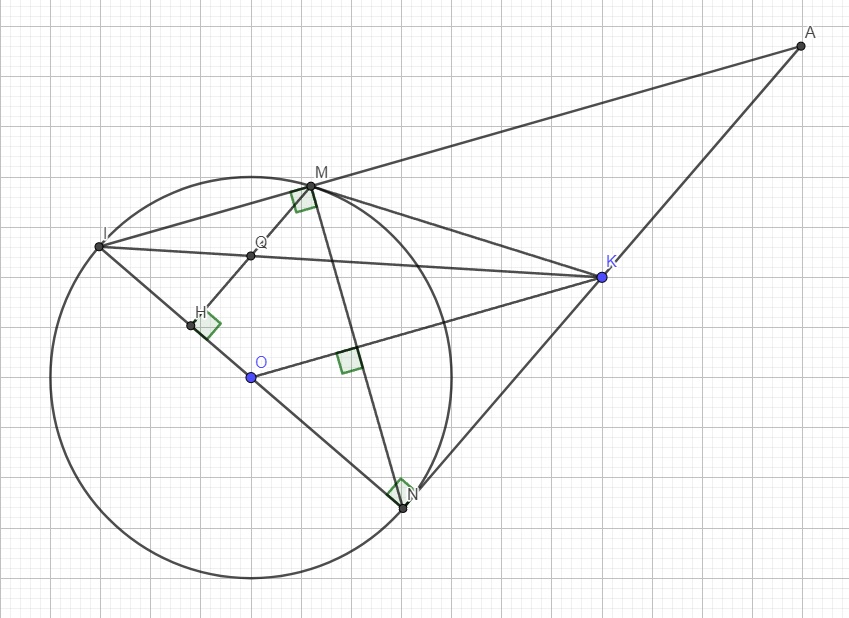
Đề bài sai nhiều quá, em kiểm tra lại câu a là ON hay MN, và câu b là ON hay MN?
a.
Ta có: \(KM=KN\) (t/c hai tiếp tuyến cắt nhau)
\(OM=ON=R\)
\(\Rightarrow OK\) là trung trực của MN, hay \(OK\perp MN\)
b.
Có \(\widehat{KMN}=\widehat{KNM}\) (do \(\Delta KMN\) cân tại K)
\(\widehat{KNM}=\widehat{HMN}\) (cùng phụ \(\widehat{HNM}\))
\(\Rightarrow\widehat{KMN}=\widehat{HMN}\)
\(\Rightarrow MN\) là phân giác \(\widehat{HMK}\)
c.
Kéo dài IM và NK cắt nhau tại A
Theo câu ta có \(OK\perp MN\Rightarrow OK||IA\) (cùng vuông góc MN)
Mà O là trung điểm IN \(\Rightarrow K\) là trung điểm AN
Hay \(KA=KN\) (1)
Do \(MH||AN\) (cùng vuông góc IN), áp dụng định lý Talet trong tam giác KIN:
\(\dfrac{IQ}{IK}=\dfrac{QH}{KN}\) (2)
Áp dụng định lý Talet trong tam giác AIK:
\(\dfrac{IQ}{IK}=\dfrac{QM}{KA}\) (3)
(1);(2);(3) \(\Rightarrow QH=QM\)