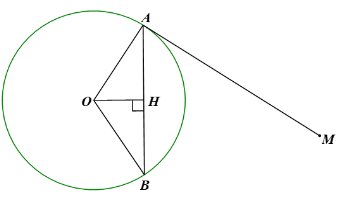
Ta có: \(OA = OB = R\) nên tam giác \(OAB\) cân tại \(O\) suy ra \(\widehat {OAB} = \widehat {OBA}\).
Xét tam giác \(OAB\) cân tại \(O\) có:
\(\begin{array}{l}\widehat {OAB} + \widehat {OBA} + \widehat {AOB} = 180^\circ \Rightarrow \widehat {OAB} + \widehat {OAB} + \widehat {AOB} = 180^\circ \\ \Rightarrow 2\widehat {OAB} = 180^\circ - \widehat {AOB} \Rightarrow \widehat {OAB} = 90^\circ - \frac{1}{2}\widehat {AOB}.\end{array}\)
Ta có: \(\widehat {OAM} = \widehat {OAB} + \widehat {BAM} = 90^\circ - \frac{1}{2}\widehat {AOB} + \frac{1}{2}\widehat {AOB} = 90^\circ .\)
Suy ra \(OA \bot AM\). Vậy \(MA\) là tiếp tuyến của đường tròn \(\left( O \right)\).
Đúng 0
Bình luận (0)


