Question

Cho đường tròn (O; 5 cm) và điểm M sao cho OM = 10 cm. Qua M vẽ hai tiếp tuyến với đường tròn tại A và B. Tính số đo góc ở tâm được tạo bởi hai tia OA và OB.

Answer 1

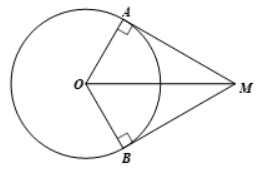
Ta có MA, MB là hai tiếp tuyến tại A và B nên \(MA \bot OA\) và \(MB \bot OB\)

Xét tam giác MAO vuông tại A, ta có:

\({\rm{cos}}\widehat {MOA} = \frac{{AO}}{{MO}} = \frac{5}{{10}} = \frac{1}{2}\)

Suy ra \(\widehat {MOA}\)= 60^o

Vì MA và MN là hai tiếp tuyến cắt nhau tại M nên OM là tia phân giác của góc AOB.

Suy ra \(\widehat {AOB} = 2\widehat {MOA} = 2.{60^o} = {120^o}\)