Cho đường tròn (O; 2cm), các tiếp tuyến AB và AC kẻ từ A đến đường tròn vuông góc với nhau tại A (B và C là các tiếp điểm)
a) Tứ giác ABOC là hình gì ? Vì sao ?
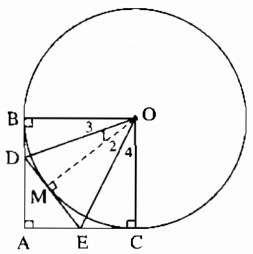
b) Gọi M là điểm bất kì thuộc cung nhỏ BC. Qua M kẻ tiếp tuyến với đường tròn, cắt AB và AC theo thứ tự tại D và E. Tính chu vi tam giác ADE ?
c) Tính số đo góc DOE ?
a) tứ giác ABOC là hình vuông
vì BAC = 90 (giả thiết)
ABO = 90 (AB là tiếp tuyến)
ACO = 90 (AC là tiếp tuyến)
AB = AC (tính chất 2 tiếp tuyến cắt nhau)
a) Ta có: AB⊥AC⇒ˆBAC=90∘AB⊥AC⇒BAC^=90∘
AB⊥BO⇒ˆABO=90∘AB⊥BO⇒ABO^=90∘
AC⊥CO⇒ˆACO=90∘AC⊥CO⇒ACO^=90∘
Tứ giác ABOC có 3 góc vuông nên nó là hình chữ nhật.
Mặt khác: AB = AC (tính chất hai tiếp tuyến cắt nhau)
Suy ra tứ giác ABOC là hình vuông.
b) Theo tính chất hai tiếp tuyến cắt nhau ta có:
DB = DM
EM = EC
Chu vi của tam giác ADE bằng:
AD + DE + EA = AD + DM + ME + EA
= AD + DB + AE + EC
= AB + AC = 2AB
Mà tứ giác ABOC là hình vuông (chứng minh trên) nên:
AB = OB = 2 (cm)
Vậy chu vi của tam giác ADE bằng: 2.2 = 4 (cm)
c) Theo tính chất hai tiếp tuyến cắt nhau ta có:
OD là tia phân giác của góc BOM
Suy ra: ˆBOD=ˆDOM=12ˆDOMBOD^=DOM^=12DOM^
OE là tia phân giác của góc COM
Suy ra: ˆCOE=ˆEOM=12ˆCOMCOE^=EOM^=12COM^
Suy ra:
ˆDOE=ˆDOM+ˆEOMDOE^=DOM^+EOM^
=12(ˆBOM+ˆCOM)=12(BOM^+COM^)
=12ˆCOB=1290∘=45∘
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22math1ed582716bfb4738ccd92405301%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%227.5%22%20y%3D%2216%22%3E%26%23x2206%3B%3C%2Ftext%3E%3C%2Fsvg%3E)
ABC đều
b) Đường vuông góc với OB tại O cắt AC tại D. Đường vuông góc với OC tại O cắt AB tại E. Chứng minh tứ giác ADOE là hình thoi
c) Chứng minh DE là tiếp điểm của đường tròn (O)