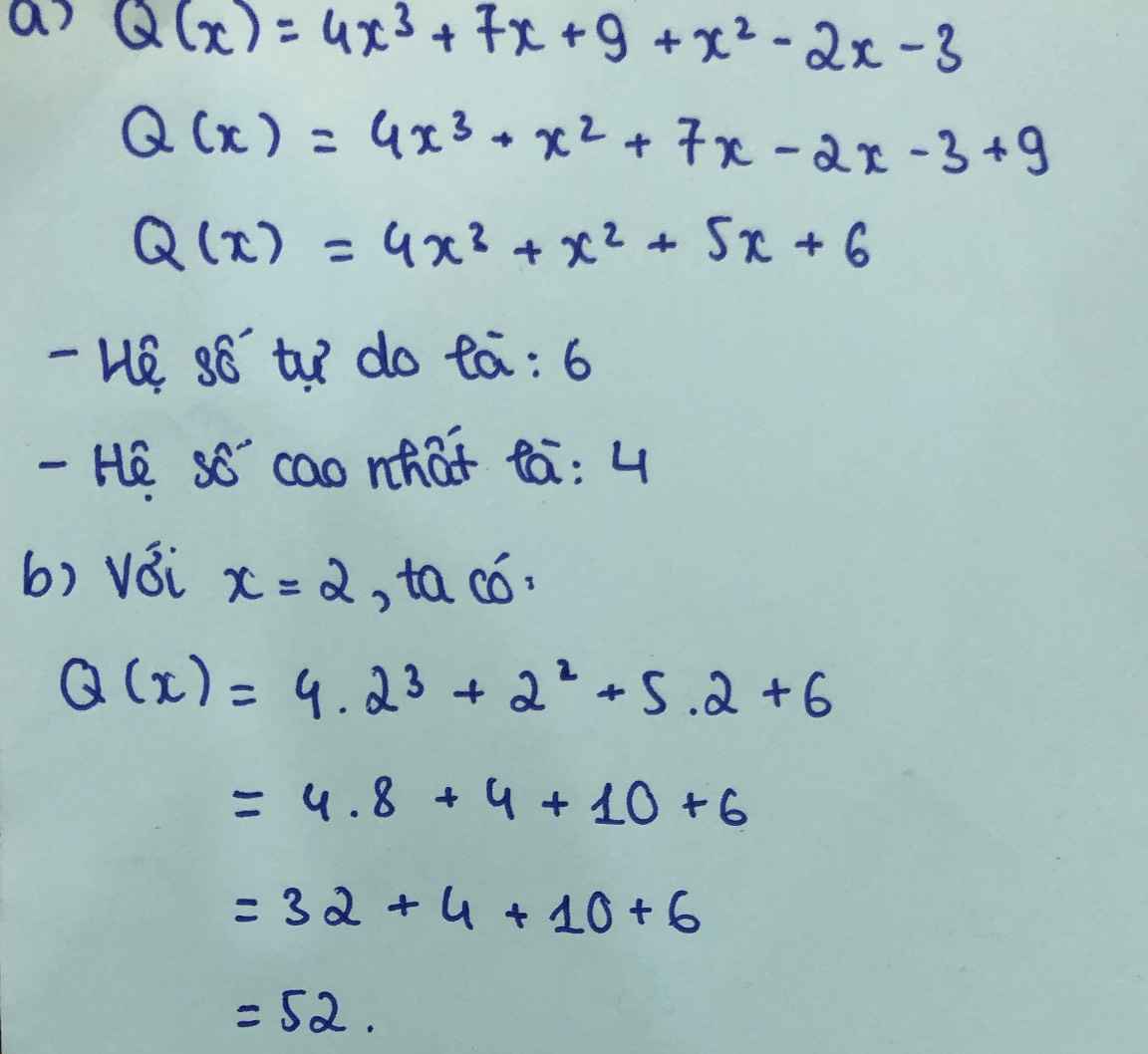a)\(Q\left(x\right)=4x^3+x^2+\left(7x-2x\right)+\left(9-3\right)=4x^3+x^2+5x+6\)
hệ số tự do : 6
hệ số cáo nhất : 6
b) thay x = 2 vào Q(x) ta đa
\(Q\left(2\right)=4.2^3+2^2+5.2+6=4.8+4+10+6\)
\(Q\left(2\right)=32+4+10+6=52\)
`a)`
`Q(x)=4x^3+7x+9+x^2-2x-3`
`Q(x)=4x^3+x^2+(7x-2x)+(9-3)`
`Q(x)=4x^3+x^2+5x+6`
`@` Hệ số tự do: `6`
`@` Hệ số cao nhất: `4`
_______________________________________
`b)` Thay `x=2` vào `Q(x)`. Có:
`Q(x)=4.2^3+2^2+5.2+6`
`Q(x)=32+4+10+6=52`
a, \(Q = 4x^3 + x^2 + (7x-2x) + (9-3) = 4x^3 + x^2 + 5x + 6 = 4x^3 + (x+2)(x+3).\)
Hệ số tự do là $6$, hệ số cao nhất là $5$.
b,Giá trị của đa thức khi $x = 2$ là:
$Q = 42^3 + (2+2)(2+3) = 32 + 4 . 5 = 52.$
Vậy khi $x = 2$ thì giá trị đa thức trên là $52$.
Q(x) = 4x2 – 2x - 3
= 4x3 + 7x - 2x + x2 + 9 - 3
= 4x3 + ( 7 - 2 )x + x2 + ( 9 - 3 )
= 4x3 + 5x + x2 + 6
Vậy Q(x) = 4x3 + 5x + x2 + 6.
- Hệ số cao nhất: 4.
- Hệ số tự do: 6.
b, Q(x) = 4x3 + 5x + x2 + 6
Với x = 2
=> Q(x) = 4x3 + 5x + x2 + 6
= 4 . 23 + 5 . 2 + 22 + 6
= 4 . 8 + 10 + 4 + 6
= 32 + 10 + 4 + 6
= 52.
Với x = 2 thì Q = 52.
a. \(Q_{\left(x\right)}=4x^3+7x+9+x^2-2x-3=4x^3+x^2+5x+6\)
Hệ số cao nhất là: 6
b. Thay x = 2 vào Q(x), ta đc:
\(4.2^3+2^2+5.2+6=52\)