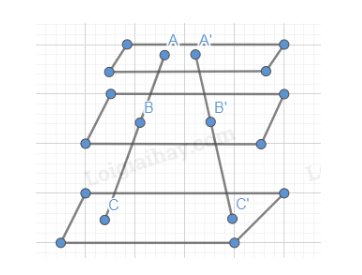
Cho ba mặt phẳng song song (P), (Q), (R). Hai cát tuyến bất kì a và a’ cắt ba mặt phẳng song song lần lượt tại các điểm A, B, C và A’, B’, C’. Gọi B1 là giao điểm của AC’ với mặt phẳng (Q) (Hình 66).
a) Nêu vị trí tương đối của BB1và CC′;B1B
và AA′
b) Có nhận xét gì về các tỉ số:
`(AB)/(AB1),(BC)/(B1C′
)và (CA)/(C′A′);(AB1)/(A′B′),(B1C′)/(B′C′)và (C′A/C′A′)`
c) Từ kết quả câu a) và câu b:, so sánh các tỉ số:
`(AB)/(A′B′),(BC)/(B′C′)và`(CA)/(C′A′)`
a) \(B{B_1}\)và\(CC'\)song song với nhau
\({B_1}B\)và\(AA'\)song song với nhau
b) Các tỉ số:
\(\frac{{AB}}{{A{B_1}}} = \frac{{BC}}{{{B_1}C'}} = \frac{{CA}}{{C'A'}}\)
\(\frac{{A{B_1}}}{{A'B'}} = \frac{{{B_1}C'}}{{B'C'}} = \frac{{C'A}}{{C'A'}}\)
c) Các tỉ số:\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}}\)