Question

Cho ba điểm A, B, C thẳng hàng sao cho B nằm giữa A và C. Chứng minh rằng độ dài của nửa đường tròn đường kính AC bằng tổng các độ dài của hai nửa đường tròn đường kính AB và BC.

Answer 1

Hướng dẫn giải:

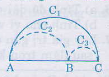
Gọi C₁, C₂, C₃ lần lượt là độ dài của các nửa đường tròn đường kính AC, AB, BC, ta có:

C₁ = π. AC (1)

C₂ = π.AB (2)

C₃ = π.BC (3)

So sánh (1), (2), (3) ta thấy:

C₂ + C_{3 =} π(AB +BC) = π. AC (vì B, nằm giữa A, C).

Vậy C₁ = C₂+C₃.

Answer 2

Gọi C₁, C₂, C₃ lần lượt là độ dài của các nửa đường tròn đường kính AC, AB, BC, ta có:

C₁ = π. AC (1)

C₂ = π.AB (2)

C₃ = π.BC (3)

So sánh (1), (2), (3) ta thấy:

C₂ + C_{3 =} π(AB +BC) = π. AC (vì B, nằm giữa A, C).

Vậy C₁ = C₂+C₃.

Answer 3

Gọi C₁, C₂, C₃ lần lượt là độ dài của các nửa đường tròn đường kính AC, AB, BC, ta có:

C₁ = π. AC (1)

C₂ = π.AB (2)

C₃ = π.BC (3)

So sánh (1), (2), (3) ta thấy:

C₂ + C_{3 =} π(AB +BC) = π. AC (vì B, nằm giữa A, C).

Vậy C₁ = C₂+C₃.