Ôn thi vào 10
Các câu hỏi tương tự
Cho tam giác ABC nhọn nội tiếp đường tròn ( O ), Đường cao AD, BE,CF cắt nhau tại H .AH ,BH, CH kéo dài cắt đường tròn tâm O lần lượt tại Q,P,R. M là trung điểm của BC, I là trung điểm của AH , EF cắt AH tại K . Chứng minh :a, Chứng minhTứ giác BFHD , CEHD , BFEC nội tiếpb, Kẻ đường kinh AN , G là trọng tâm . Chứng minh H,G,O thẳng hàngc, Chứng minh P,Q,R đối xứng với H qua AC,BC,ABd, Chứng minh OA vuông góc với EF và tam giác ARQ câne, EF cắt đường tròn tại E1 và F1. Chứng minh AE1 , AF1 là ti...
Đọc tiếp
Cho tam giác ABC nhọn nội tiếp đường tròn ( O ), Đường cao AD, BE,CF cắt nhau tại H .AH ,BH, CH kéo dài cắt đường tròn tâm O lần lượt tại Q,P,R. M là trung điểm của BC, I là trung điểm của AH , EF cắt AH tại K . Chứng minh :
a, Chứng minhTứ giác BFHD , CEHD , BFEC nội tiếp
b, Kẻ đường kinh AN , G là trọng tâm . Chứng minh H,G,O thẳng hàng
c, Chứng minh P,Q,R đối xứng với H qua AC,BC,AB
d, Chứng minh OA vuông góc với EF và tam giác ARQ cân
e, EF cắt đường tròn tại E1 và F1. Chứng minh AE1 , AF1 là tiếp tuyến của đường tròn ngoại tiếp tam giác CEE1 và tam giác BFF1
f, Chứng minh K là trực tâm của tam giác IBC
h,Chứng minh ME và MF là tiếp tuyến của đường tròn ngoại tiếp tam giác AEF
bài 8/77
cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn ,các đường cao AI < BK của tam giác ABC cắt nhau tại H ( I thuộc BC , K thuộc AC ) .AI vad BK cắt đường tròn O lần lượt tại D và E
A/chứng minh tứ giác ABIK nội tiếp
B/ gọi M là trung điểm của DE . chứng minh 3 điểm O,M,C thẳng hàng
C/chứng mình IK song song ED
thankkkkk
cho △ABC nhọn nội tiếp đường tròn (o) có hai đường cao BD và CE cắt nhau tại H.
a) chứng minh 4 điểm B,C,D,E cùng thuôc 1 đường tròn.
b) chứng minh DE⊥OA.
c) cho M , N lần lượt là trung điểm của 2 đoạn thẳng AC , BH. cho K, L lần lượt là giao điểm của 2 đường thẳng OM và CE, MN và BD. chứng minh KL song song với AC.
cho tam giác abc nhọn nội tiếp đường tròn o với các tiếp điểm là e,f,n(e thuộc ab, f thuộc ac, n thuộc bc) kẻ đường kính nm tiếp tuyến tâm o qua m cắt ab ac lần lượt tại d và i an cắt di tại k cm dk/ki=be/cf
Cho tam giác nhọn ABC nội tiếp đường tròn ( O ; R ) Hai đường cao AD BE ( D thuộc BC E thuộc AC ) lần lượt cắt đường tròn (O) tại các điểm thứ hai là M và Na) Chứng minh: CDHE,AEDB là tứ giác nội tiếp đường trònb) Chứng minh MN // DEc) Cho (O) và dây AB cố định Chứng minh rẳng độ dài bán kính đường tròn ngoại tiếp tam giác CDE luôn không đổi khi điểm C di chuyển trên cung lớn
Đọc tiếp
Cho tam giác nhọn ABC nội tiếp đường tròn ( O ; R ) Hai đường cao AD BE ( D thuộc BC E thuộc AC ) lần lượt cắt đường tròn (O) tại các điểm thứ hai là M và N
a) Chứng minh: CDHE,AEDB là tứ giác nội tiếp đường tròn
b) Chứng minh MN // DE
c) Cho (O) và dây AB cố định Chứng minh rẳng độ dài bán kính đường tròn ngoại tiếp tam giác CDE luôn không đổi khi điểm C di chuyển trên cung lớn
Cho DeltaABC có widehat{A}90^0, đường cao AH (H in BC), biết BH 4cm, CH 9cm. Kẻ HD bot AB, HE bot
AC (D in AB, E in AC).b) Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH.c) tính diện tích của tứ giác DEMN.
Đọc tiếp
Cho \(\Delta\)\(ABC\) có \(\widehat{A}\)\(=90^0\), đường cao AH (H \(\in\) BC), biết BH = 4cm, CH = 9cm. Kẻ HD \(\bot\) AB, HE \(\bot \) AC (D \(\in\) AB, E \(\in\) AC).
b) Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH.
c) tính diện tích của tứ giác DEMN.
Cho tam giác ABC vuông tại A có AC>AB. Gọi I là tâm đường tròn nội tiếp tam giác ABC, các tiếp điểm của đường tròn nội tiếp với các cạnh AB,BC,CA lần lượt tại M,N,P.
a) Chứng minh tứ giác AMIP là hình vuông
b) Đường thẳng AI cắt PN tại D. Chứng minh 5 điểm M,B,N,O,I nằm trên một đường tròn
Cho tam giác ABC có cạnh AB AC. Các đường cao AD và BE của tam giác ABC cắt nhau tại H. Gọi I đối xứng với H qua D. Gọi M và N lần lượt là hình chiếu vuông góc của I trên AB và AC.a) Chứng minh tứ giác ABDE nội tiếp và góc widehat{CAD}widehat{CBI} ?b) Chứng minh rằng góc widehat{MDI}widehat{ACI} và tam giác ACI đồng dạng với tam giác MDI ?c) Gọi P và Q lần lượt là trung điểm của MD và AC. Chứng minh rằng góc widehat{IPQ}90^0 ?P/s: Nhờ thầy cô và các bạn giúp đỡ ý c với ạ, cám ơn n...
Đọc tiếp
Cho tam giác ABC có cạnh AB < AC. Các đường cao AD và BE của tam giác ABC cắt nhau tại H. Gọi I đối xứng với H qua D. Gọi M và N lần lượt là hình chiếu vuông góc của I trên AB và AC.
a) Chứng minh tứ giác ABDE nội tiếp và góc \(\widehat{CAD}=\widehat{CBI}\) ?
b) Chứng minh rằng góc \(\widehat{MDI}=\widehat{ACI}\) và tam giác ACI đồng dạng với tam giác MDI ?
c) Gọi P và Q lần lượt là trung điểm của MD và AC. Chứng minh rằng góc \(\widehat{IPQ}=90^0\) ?
P/s: Nhờ thầy cô và các bạn giúp đỡ ý c với ạ, cám ơn nhiều ạ!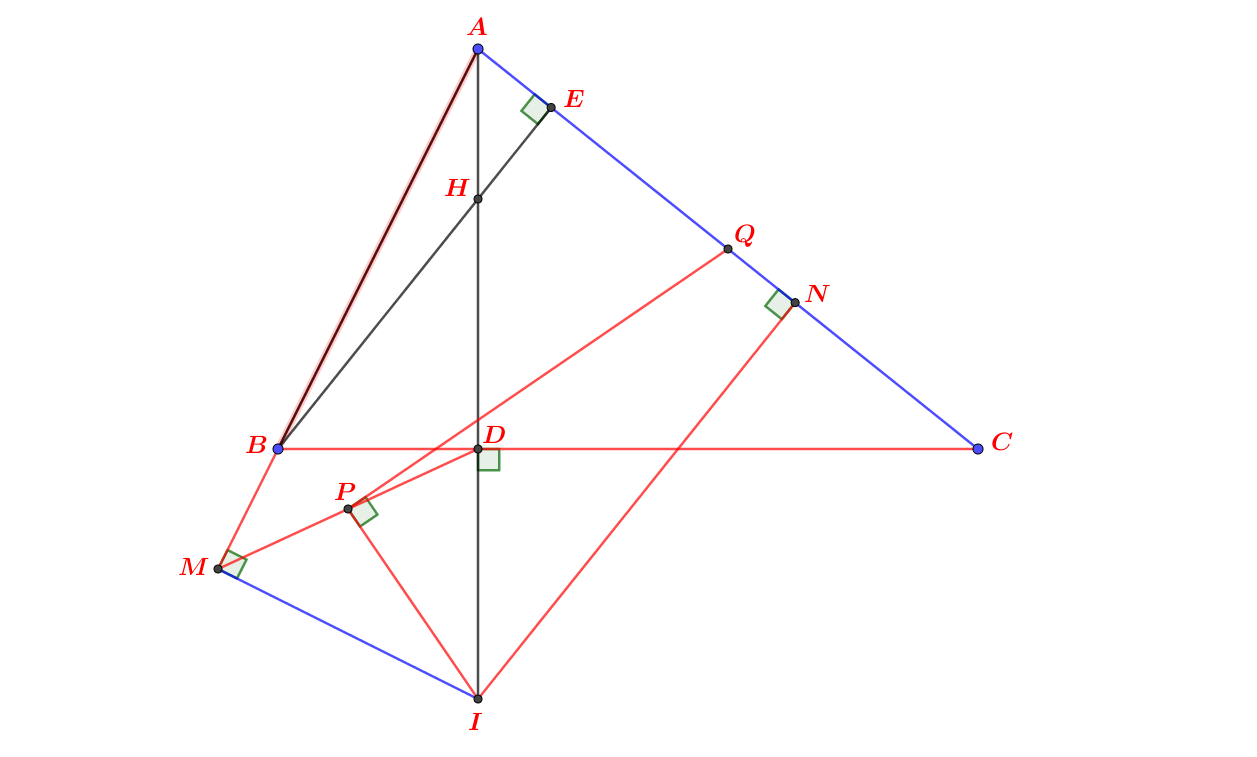
Tam giác ABC nội tiếp đường tròn (T) có tâm O có AB =AC và góc BAC > 90 độ. Gọi M là trung điểm AC, tia MO cắt (T) tại D, BC lần lượt cắt AO và AD tại N và P.
a) Phân giác góc BDP cắt BC tại E, ME cắt AB tại F. Chứng minh CA =CP và ME vuông góc với DB
b ) Chứng minh tam giác MNE cân, tính tỉ số DE/DF











