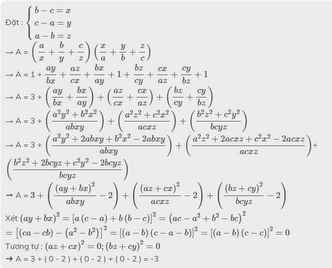Ôn tập toán 8
Các câu hỏi tương tự
cho các số a,b,c khác 0 thỏa mãn a+b+c=1 và 1/a+1/b+1/c=0 .tính giá trị của biểu thức P= (a2+b2+c2)(bc/a2 +ca/b2 +ab/c2).
Cho các số thực a,b,c đôi một khác nhau thỏa mãn \(\left(a-b\right)\sqrt[3]{1-c^3}+\left(b-c\right)\sqrt[3]{1-a^3}+\left(c-a\right)\sqrt[3]{1-b^3}=0\)
Chứng minh rằng \(\sqrt[3]{\left(1-a^3\right)\left(1-b^3\right)\left(1-c^3\right)}+abc=1\)
a)Tìm hai số chẵn liên tiếp mà hiệu các lập phương của hai số đó bằng 2012
b)Cho 2012 số thực khác nhau. Biết tích của 13 số bất ký trong 2012 số đó luôn là một số dương. C/m 2012 số đó đều dương
c)Cho 5 số nguyên khác không:a, b, c,d,k và abc/dk<0. Ss (bcd/ka)+(cdk/ab)+(dka/bc) và số 0
d)Cho biết tồn tại hai số thực a, b thỏa a+b=2 và a^3+b^3=14. Tìm giá trị a^5+b^5
cho a,b,c,d là các ố nguyên dương đôi một khác nhau thỏa mản \(\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+d}+\frac{d}{a+d}=2\)
CMR abcd là số chính phương
cho a,b,c là các số thực thỏa mãn : \(a+b+c=2014\) và \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{2014}\)
tính giá trị của biểu thức : \(M=\frac{1}{a^{2013}}+\frac{1}{b^{2013}}+\frac{1}{c^{2013}}\)
Cho 3 số thực khác nhau và khác 0 là a,b,c thỏa mãn \(a+b+c=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\) . Chứng ming :
\(\frac{bc-a^2}{a\left(bc-1\right)}=\frac{b^2-ac}{b\left(1-ac\right)}\)
@Lê Trịnh Việt Tiến GIẢI ĐI
Cho các số a,b,c thỏa mãn điều kiện: a2+b2+c2=1 và a3+b3+c3=1.
Tính giá trị của biểu thức: S=a2+b9+c1945
b)Cho a,b,c,d là các số khác 0 và (a+b+c+d)(a-b-c+d)=(a-b+c-d)(a+b-c-d)
Cmr:\(\frac{a}{c}=\frac{b}{d}\)
cho 3 số a,b,c có tổng khác 0 thỏa mãn: a(a² -bc) + b(b² – ca) + c (c² – ab) = 0 Tính giá trị của biểu thức:
P = \(\frac{a^2}{b^2}+\frac{b^2}{c^2}+\frac{c^2}{a^2}\)