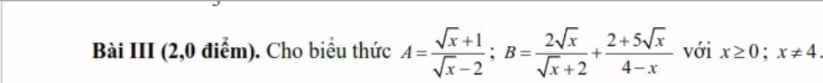\(A=\) \(\frac{2\sqrt{x}-1}{\sqrt{x}+2}=\frac{2\left(\sqrt{x}+2\right)-5}{\sqrt{x}+2}=2-\frac{5}{\sqrt{x}+2}\)\(\ge2-\frac{5}{2}=\frac{-1}{2}\)
mặt khác \(A=2-\frac{5}{\sqrt{x}+2}\le2\)
\(\Rightarrow\frac{-1}{2}\le A< 2\). Vì \(A\in Z\)nên \(\left[{}\begin{matrix}A=0\\A=1\end{matrix}\right.\)
đến đây thay vào giải là được
Bài 1:Tìm x để BT có giá trị nguyên:
\(\dfrac{3\sqrt{x}+1}{2\sqrt{x}-1}\)
Bài 2:Cho A =\(\dfrac{2\sqrt{x}+1}{x+1}\)(với x≥0).Tìm x để A có giá trị nguyên
Bài 8. Cho M = \(\dfrac{\sqrt{x}+5}{\sqrt{x}+1}\) với 𝑥 ≥ 0; 𝑥 ≠ 1. Tìm số thực x để M có giá trị nguyên
Bài 9. Cho P = \(\dfrac{\sqrt{x}+7}{\sqrt{x}+2}\) với x ≥ 0; x ≠ 1. Tìm các số thực x để P có giá trị là số nguyên.
Bài 8:Cho A=\(\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)và B=\(\dfrac{\sqrt{x}+3}{\sqrt{x}+1}-\dfrac{5}{1-\sqrt{x}}+\dfrac{4}{x-1}\)(x≥0;x≠1)
a)Tính giá trị của A khi x=\(4+2\sqrt{3}\)
b)Rút gọn B
c)Tìm x để P=A.B có giá trị nguyên
Bài 5. Cho biểu thức: C = \(\dfrac{2\sqrt{x}-3}{\sqrt{x}-2}\) 𝑣ớ𝑖 𝑥 ≥ 0; 𝑥 ≠ 4. Tìm x nguyên để C đạt giá trị nguyên nhỏ nhất
Bài 6. Cho biểu thức: D = \(\dfrac{x-3}{\sqrt{x}+1}\) với 𝑥 ≥ 0; 𝑥 ≠ 1. Tìm x nguyên để D có giá trị là số nguyên
Bài 2:Cho A =\(\dfrac{2\sqrt{x}+1}{x+1}\)(với x≥0).Tìm x để A có giá trị nguyên
Bài 2:Cho A =\(\dfrac{2\sqrt{x}+1}{x+1}\)(với x≥0).Tìm x để A có giá trị nguyên
Bài 10. Cho biểu thức P = \(\dfrac{2\sqrt{x-3}}{\sqrt{x}+2}\) với 𝑥 ≥ 0; 𝑥 ≠ 4. Tìm các giá trị của x để P có giá trị nguyên.
Câu 1: Rút gọn
\(\dfrac{2}{\sqrt{5}-\sqrt{3}}+\dfrac{3}{\sqrt{6}+\sqrt{3}}\)
Câu 2:
Cho A= \(\dfrac{1}{x-2\sqrt{x-5}+3}\). Tìm giá trị lớn nhất của A, giá trị đó đạt được khi x bằng bao nhiêu?
Ctv giúp em làm câu này với.
Câu hỏi : Tìm giá trị nguyên lớn nhất của x để P có giá trị nguyên.
Biết rằng : P = \frac{3\sqrt{x}}{\sqrt{x}+2}
A = \(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{4}{x-2\sqrt{x}}\) với x > 0, và x \(\ne\) 4
a) Rút gọn A
b) So sánh A với 1.
c) Tìm tất cả các giá trị nguyên để A nhận giá trị nguyên.
