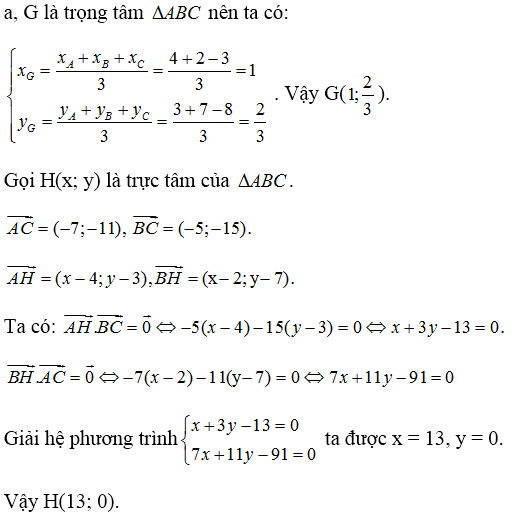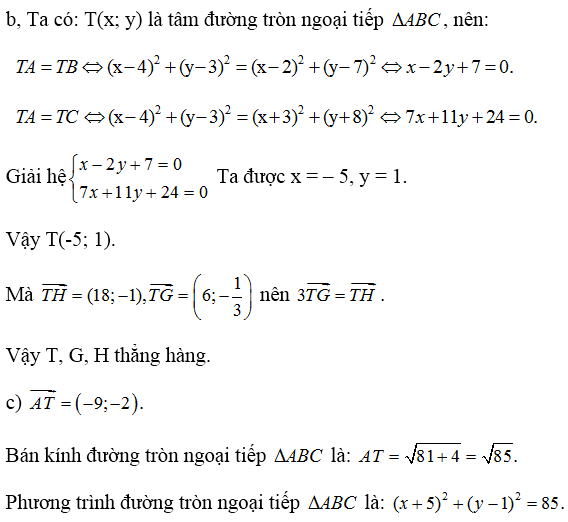Ôn tập chương III
Các câu hỏi tương tự
Cho ba điểm \(A\left(2;1\right);B\left(0;5\right);C\left(-5;-10\right)\)
a) Tìm tọa độ trọng tâm G, trực tâm H và tâm I đường tròn ngoại tiếp tam giác ABC
b) Chứng minh I, G, H thẳng hàng
c) Viết phương trình đường tròn ngoại tiếp tam giác ABC
Cho ba điểm \(A\left(3;5\right);B\left(2;3\right);C\left(6;2\right)\)
a) Viết phương trình đường tròn (C) ngoại tiếp tam giác ABC
b) Hãy xác định tọa độ của tâm và bán kính của (C)
Trong mặt phẳng tọa đọ Oxy cho điểm Mleft(2;dfrac{3}{2}right)
a) Viết phương trình đường tròn (C) có đường kính OM
b) Viết phương trình đường thẳng d đi qua M và cắt hai nửa trục dương Ox, Oy lần lượt tại A, B sao cho diện tích tam giác OAB bằng 6 đơn vị diện tích
c) Tìm tọa độ tâm I của đường tròn nội tiếp (T) của tam giác OAB. Viết phương trình đường tròn đó
Đọc tiếp
Trong mặt phẳng tọa đọ Oxy cho điểm \(M\left(2;\dfrac{3}{2}\right)\)
a) Viết phương trình đường tròn (C) có đường kính OM
b) Viết phương trình đường thẳng d đi qua M và cắt hai nửa trục dương Ox, Oy lần lượt tại A, B sao cho diện tích tam giác OAB bằng 6 đơn vị diện tích
c) Tìm tọa độ tâm I của đường tròn nội tiếp (T) của tam giác OAB. Viết phương trình đường tròn đó
Trong mặt phẳng tọa đọ Oxy, xét tam giác ABC vuông tại A, phương trình đường thẳng BC là : \(\sqrt{3}x-y-\sqrt{3}\), các đỉnh A và B thuộc trục hoành và bán kính đường tròn nội tiếp tam giác bằng 2. Tìm tọa độ trọng tâm G của tam giác ABC
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có \(A\left(0;2\right);B\left(-2;2\right);C\left(4;-2\right)\). Gọi H là chân đường cao kẻ từ B, M và N lần lượt là trung điểm của các cạnh AB và BC. Viết phương trình đường tròn đi qua các điểm H, M, N
Trong mặt phẳng Oxy, cho tam giác ABC có 3 đỉnh \(A\left(1;-1\right);B\left(2;-3\right);C\left(3;3\right)\)
a) Tìm số đo của góc A của tam giác ABC
b) Viết phương trình các cạnh AB, AC
c) Viết phương trình đường phân giác trong góc A của tam giác ABC
Trong mặt phẳng tọa độ Oxy cho hai điểm \(A\left(2;0\right);B\left(6;4\right)\). Viết phương trình đường tròn (C) tiếp xúc với trục hoành tại điểm A và khoảng cách từ tâm của (C) đến điểm B bằng 5
Trong mặt phẳng tọa độ Oxy, hãy xác định tọa độ đỉnh C của tam giác ABC biết rằng hình chiếu vuông góc của C trên đường thẳng AB là điểm \(H\left(-1;-1\right)\), đường phân giác trong góc A có phương trình \(x-y+2=0\) và đường cao kẻ từ B có phương trình \(4x+3y-1=0\)
Trong một mặt phẳng Oxy cho điểm M(6;0) và đường thẳng \(\left(\Delta\right)\) : x+2y-9=0
a,Tính khoảng cách từ M đến \(\left(\Delta\right)\)
b, Viết phương trình đường tròn tâm M và tiếp xúc với \(\left(\Delta\right)\)