a) \(\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
Đặt: \(x^2+x+1=y\), khi đó biểu thức trở thành:
\(y\left(y+1\right)-12\)
\(=y^2+y-12\)
\(=y^2-3y+4y-12\)
\(=y\left(y-3\right)+4\left(y-3\right)\)
\(=\left(y-3\right)\left(y+4\right)\)
\(=\left(x^2+x+1-3\right)\left(x^2+x+1+4\right)\)
\(=\left(x^2+x-2\right)\left(x^2+x+5\right)\)
\(=\left(x^2-x+2x-2\right)\left(x^2+x+5\right)\)
\(=\left[x\left(x-1\right)+2\left(x-1\right)\right]\left(x^2+x+5\right)\)
\(=\left(x-1\right)\left(x+2\right)\left(x^2+x+5\right)\)
b) \(\left(x^2+2x\right)^2+9x^2+18x+20\)
\(=\left(x^2+2x\right)^2+9\left(x^2+2x\right)+20\)
Đặt: \(x^2+2x=a\), khi đó biểu thức trở thành:
\(a^2+9a+20\)
\(=a^2+4a+5a+20\)
\(=a\left(a+4\right)+5\left(a+4\right)\)
\(=\left(a+4\right)\left(a+5\right)\)
\(=\left(x^2+2x+4\right)\left(x^2+2x+5\right)\)
c) \(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)+16\)
\(=\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]+16\)
\(=\left(x^2+10x+16\right)\left(x^2+10x+24\right)+16\)
Đặt: \(x^2+10x+20=y\), khi đó biểu thức trở thành:
\(\left(y-4\right)\left(y+4\right)+16\)
\(=y^2-16+16\)
\(=y^2\)
\(=\left(x^2+10x+20\right)^2\)
$\text{#}Toru$
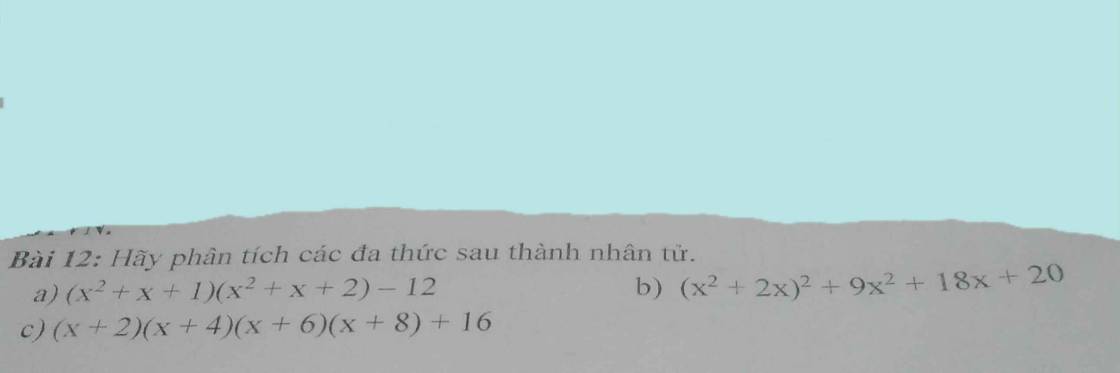
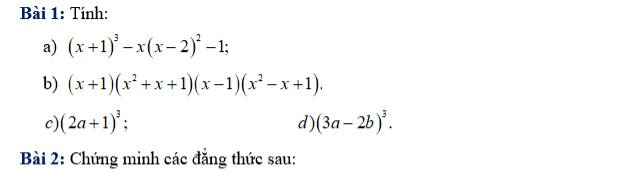
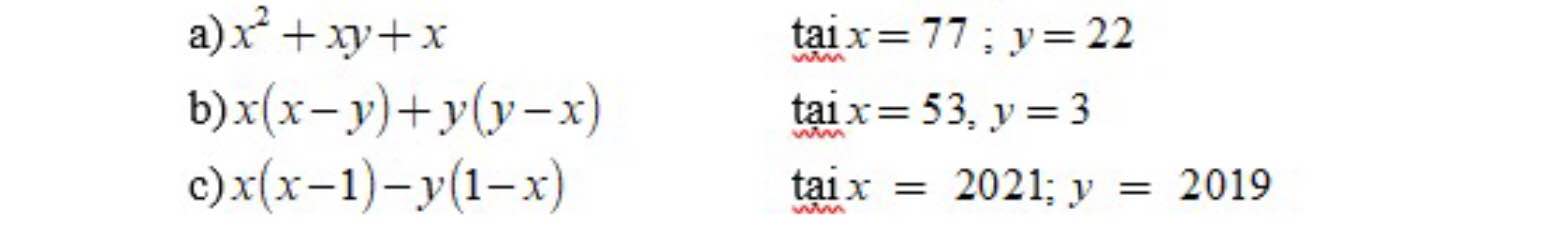bài này nữa thôi các anh chị :3 em cảm ơn nhiều ạ
