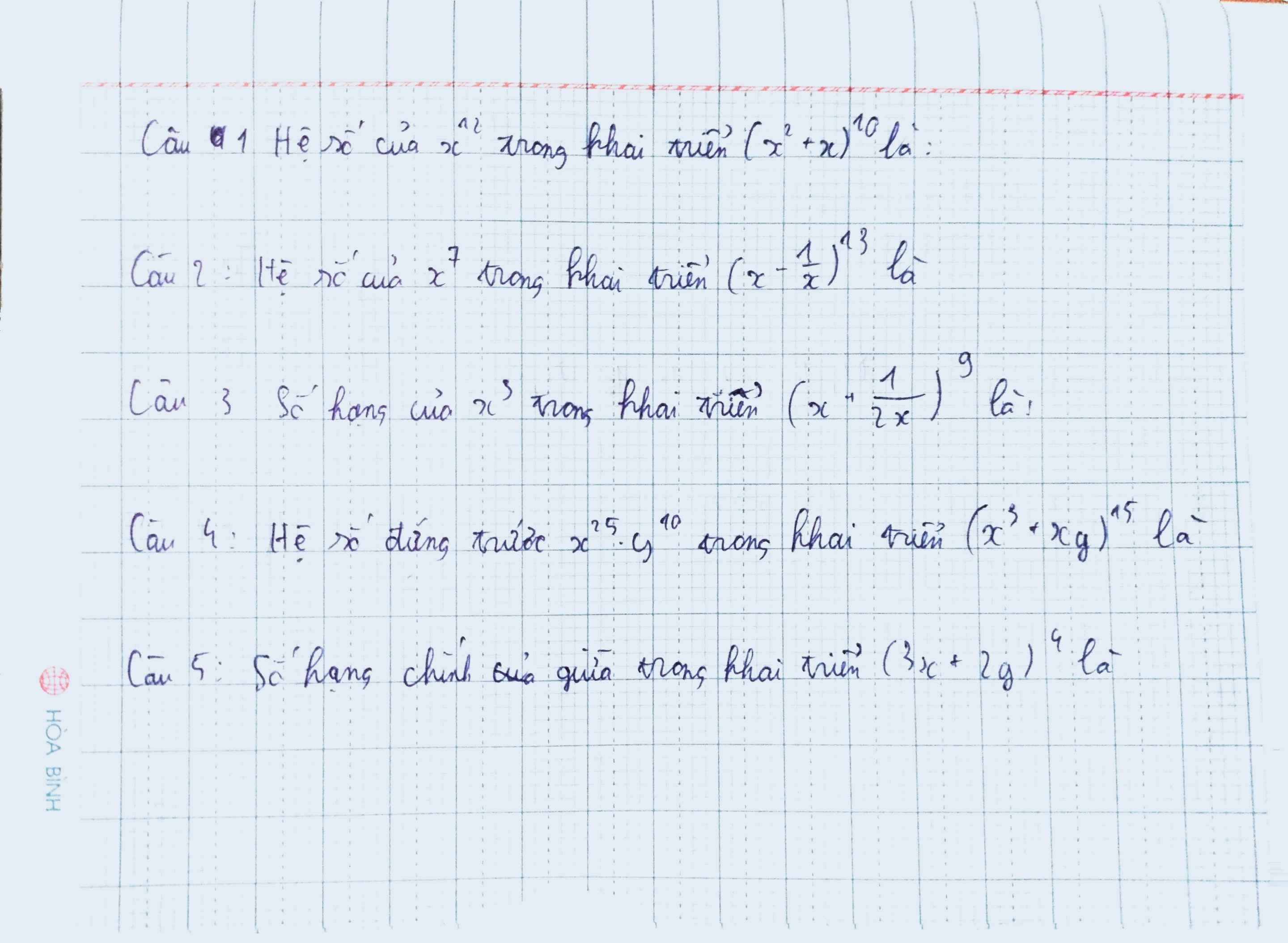1.
\(\left(x^2+x\right)^{10}=\sum\limits^{10}_{k=0}C^k_{10}.\left(x^2\right)^{10-k}.x^k=\sum\limits^{10}_{k=0}C^k_{10}.x^{20-k}\)
\(\Rightarrow20-k=12\Rightarrow k=8\)
\(\Rightarrow\) Hệ số của \(x^{12}\) trong khai triển \(\left(x^2+x\right)^{10}\) là: \(C^8_{10}=45\)
2.
\(\left(x-\dfrac{1}{x}\right)^{13}=\sum\limits^{13}_{k=0}C^k_{13}.x^{13-k}.\dfrac{1}{x^k}=\sum\limits^{13}_{k=0}C^k_{13}.x^{13-2k}\)
\(\Rightarrow13-2k=7\Rightarrow k=3\)
\(\Rightarrow\) Hệ số của \(x^7\) trong khai triển \(\left(x-\dfrac{1}{x}\right)^{13}\) là: \(C^3_{13}=286\)
3.
\(\left(x+\dfrac{1}{2x}\right)^9=\sum\limits^9_{k=0}C^k_9.x^{9-k}.\dfrac{1}{2^k.x^k}=\sum\limits^9_{k=0}\dfrac{C^k_9}{2^k}.x^{9-2k}\)
\(\Rightarrow9-2k=3\Rightarrow k=3\)
\(\Rightarrow\) Hệ số của \(x^3\) trong khai triển \(\left(x+\dfrac{1}{2x}\right)^9\) là: \(\dfrac{C^3_9}{2^3}=\dfrac{21}{2}\)
4.
\(T_{k+1}=C^k_{15}\left(x^3\right)^{15-k}.\left(xy\right)^k\)
\(\Rightarrow\left\{{}\begin{matrix}15-k=6\\k=9\end{matrix}\right.\Rightarrow k=9\)
\(\Rightarrow\) Hệ số đứng trước \(x^{25}y^{10}\) là: \(C^9_{15}=5005\)
5.
Số hạng tổng quát của khai triển \(\left(3x+2y\right)^4\) là: \(C^k_4.3^{4-k}.2^k.x^{4-k}.y^k\)
\(\Rightarrow k=3\)
\(\Rightarrow\) Số hạng chính giữa trong khai triển \(\left(3x+2y\right)^4\) là: \(C^3_4.3.2^3.x.y^3=96xy^3\)