Question

Câu 1: phần hai b

Answer 1

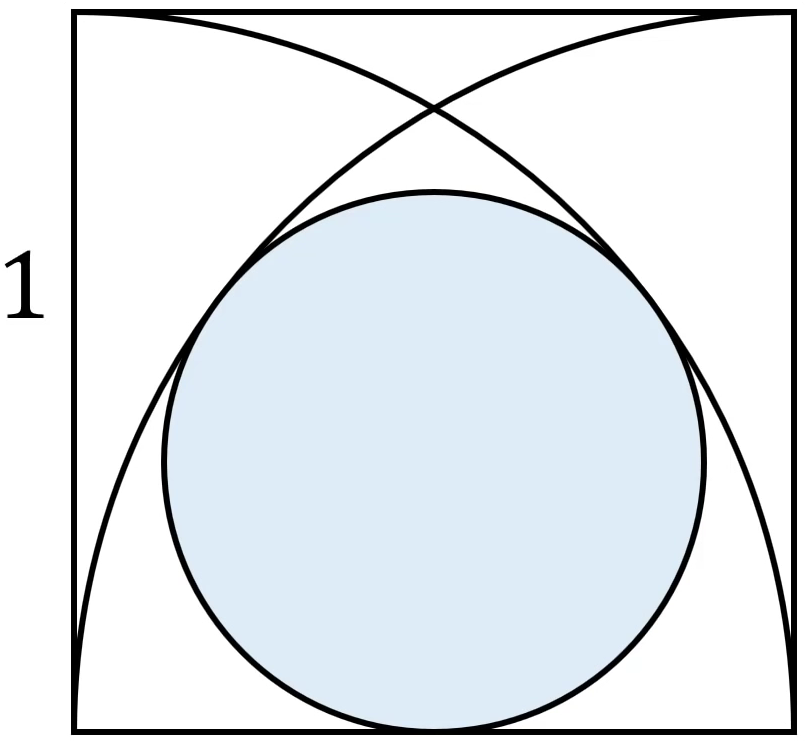
Bài 1:

2:

a) Ta có: \(M=\left(1+\frac{\sqrt{a}}{a+1}\right):\left(\frac{1}{\sqrt{a}-1}-\frac{2\sqrt{a}}{a\sqrt{a}+\sqrt{a}-a-1}\right)\)

\(=\left(\frac{a+1+\sqrt{a}}{a+1}\right):\left(\frac{a+1}{\left(a+1\right)\left(\sqrt{a}-1\right)}-\frac{2\sqrt{a}}{\left(a+1\right)\left(\sqrt{a}-1\right)}\right)\)

\(=\frac{a+1+\sqrt{a}}{a+1}:\frac{\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}-1\right)\left(a+1\right)}\)

\(=\frac{a+\sqrt{a}+1}{a+1}:\frac{\sqrt{a}-1}{a+1}\)

\(=\frac{a+\sqrt{a}+1}{\sqrt{a}-1}\)

b) Để M>1 thì \(\frac{a+\sqrt{a}+1}{\sqrt{a}-1}>1\)

\(\Leftrightarrow a+\sqrt{a}+1>\sqrt{a}-1\)

\(\Leftrightarrow a+\sqrt{a}+1-\sqrt{a}+1>0\)

\(\Leftrightarrow a+2>0\)

\(\Leftrightarrow a>-2\)

mà \(a\ge0\left(đkxđ\right)\)

nên \(a\ge0\)

Vậy: Khi a không âm và a\(\ne\)1 thì M>1

Answer 2

https://i.imgur.com/ibXXfG8.jpg