Bài 19:
Xét ΔAMB có MK là đường phân giác ứng với cạnh AB(gt)
nên \(\dfrac{AM}{MB}=\dfrac{AK}{KB}\)(Tính chất tia phân giác của tam giác)(1)
Xét ΔAMC có MH là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AM}{MC}=\dfrac{AH}{HC}\)(Tính chất tia phân giác của tam giác)(2)
Ta có: MB=MC(M là trung điểm của BC)
nên \(\dfrac{AM}{MB}=\dfrac{AM}{MC}\)(3)
Từ (1), (2) và (3) suy ra \(\dfrac{AK}{KB}=\dfrac{AH}{HC}\)
Xét ΔABC có
K\(\in\)AB(gt)
H\(\in\)AC(gt)
\(\dfrac{AK}{KB}=\dfrac{AH}{HC}\)(cmt)
Do đó: HK//BC(Định lí Ta lét đảo)







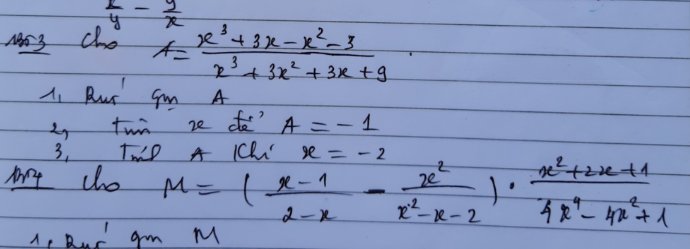
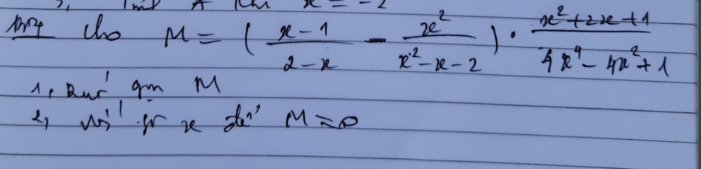




 mn giup mik bai 3 nay dc ko aj
mn giup mik bai 3 nay dc ko aj