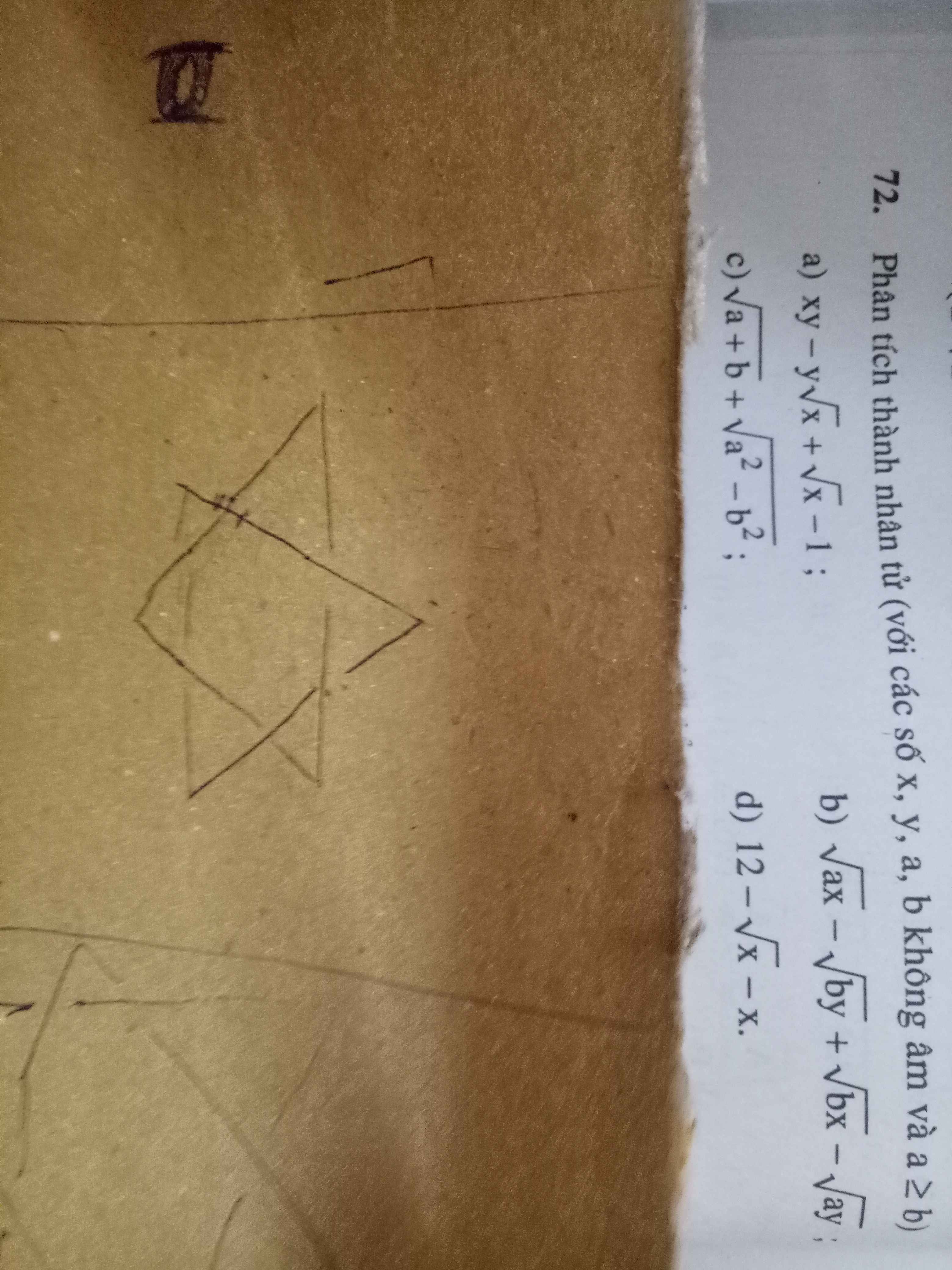a) \(xy-y\sqrt{x}+\sqrt{x}-1=y\sqrt{x}\left(\sqrt{x}-1\right)+\sqrt{x}-1\)
\(=\left(\sqrt{x}-1\right)\left(y\sqrt{x}+1\right)\)
b) \(\sqrt{ax}-\sqrt{by}+\sqrt{bx}-\sqrt{ay}=\sqrt{a}\left(\sqrt{x}-\sqrt{y}\right)+\sqrt{b}\left(\sqrt{x}-\sqrt{y}\right)\)
\(=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{a}+\sqrt{b}\right)\)
c) \(\sqrt{a+b}+\sqrt{a^2-b^2}=\sqrt{a+b}\left(\sqrt{a-b}+1\right)\)
d) \(12-\sqrt{x}-x=-\left(x+\sqrt{x}-12\right)=-\left(x-3\sqrt{x}+4\sqrt{x}-12\right)\)
\(=-\left(\sqrt{x}\left(\sqrt{x}-3\right)+4\left(\sqrt{x}-3\right)\right)=-\left(\sqrt{x}+4\right)\left(\sqrt{x}-3\right)\)
\(=\left(3-\sqrt{x}\right)\left(\sqrt{x}+4\right)\)
a) Ta có: \(xy-y\sqrt{x}+\sqrt{x}-1\)
\(=y\sqrt{x}\left(\sqrt{x}-1\right)+\left(\sqrt{x}-1\right)\)
\(=\left(\sqrt{x}-1\right)\left(y\sqrt{x}+1\right)\)
b) Ta có: \(\sqrt{ax}-\sqrt{by}+\sqrt{bx}-\sqrt{ay}\)
\(=\sqrt{a}\left(\sqrt{x}-\sqrt{y}\right)+\sqrt{b}\left(\sqrt{x}-\sqrt{y}\right)\)
\(=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{a}+\sqrt{b}\right)\)
c) Ta có: \(\sqrt{a+b}+\sqrt{a^2-b^2}\)
\(=\sqrt{a+b}+\sqrt{a+b}\cdot\sqrt{a-b}\)
\(=\sqrt{a+b}\left(1+\sqrt{a-b}\right)\)
d) Ta có: \(12-\sqrt{x}-x\)
\(=12-4\sqrt{x}+3\sqrt{x}-x\)
\(=4\left(3-\sqrt{x}\right)+\sqrt{x}\left(3-\sqrt{x}\right)\)
\(=\left(3-\sqrt{x}\right)\left(\sqrt{x}+4\right)\)