\(25{x^2} + 20xy + 4{y^2} = {\left( {5x} \right)^2} + 2.5x.2y + {\left( {2y} \right)^2} = {\left( {5x + 2y} \right)^2}\)
Chọn D.
\(25{x^2} + 20xy + 4{y^2} = {\left( {5x} \right)^2} + 2.5x.2y + {\left( {2y} \right)^2} = {\left( {5x + 2y} \right)^2}\)
Chọn D.
Rút gọn các biểu thức:
a) \(\left( {2x - 5y} \right)\left( {2x + 5y} \right) + {\left( {2x + 5y} \right)^2}\)
b) \(\left( {x + 2y} \right)\left( {{x^2} - 2xy + 4{y^2}} \right) + \left( {2x - y} \right)\left( {4{x^2} + 2xy + {y^2}} \right)\)
Rút gọn biểu thức \(A = {\left( {2x + 1} \right)^3} - 6x\left( {2x + 1} \right)\) ta được
A. \({x^3} + 8\)
B. \({x^3} + 1\)
C. \(8{x^3} + 1\)
D. \(8{x^3} - 1\)
Phân tích các đa thức sau thành nhân tử:
a) \(6{x^2} - 24{y^2}\)
b) \(64{x^3} - 27{y^3}\)
c) \({x^4} - 2{x^3} + {x^2}\)
d) \({\left( {x - y} \right)^3} + 8{y^3}\)
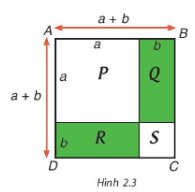
Sử dụng Hình 2.3, bằng cách tính diện tích hình vuông ABCD theo hai cách, hãy giải thích hằng đẳng thức \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\).
Tính nhanh giá trị của các biểu thức:
a) \({x^2} - 4x + 4\) tại x=102.
b) \({x^3} + 3{x^2} + 3x + 1\) tại x=999.