Question

Bạn Lan muốn cắt hình ngôi sao có dạng như Hình 9.62 (trong đó ABCDE là một ngũ giác đều). Lan gấp đôi tờ giấy, vẽ một nửa ngôi sao và cắt theo nét vẽ. Hỏi góc tạo bởi lưỡi kéo và nếp gấp lúc đầu bằng bao nhiêu độ?

Answer 1

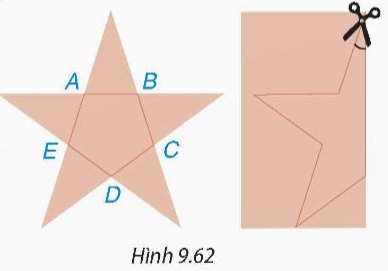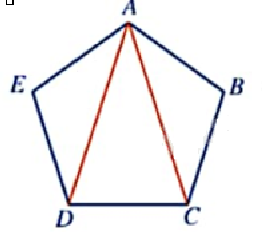
Xét ngũ giác đều ABCDE, ta thấy tổng 5 góc của ngũ giác đều đó bằng tổng các góc trong ba tam giác ABC, ACD, ADE, tức là bằng \({3.180^o} = {540^o}\). Do tất cả các góc của ngũ giác đều bằng nhau nên số đo mỗi góc của ngũ giác đều bằng \(\frac{{{{540}^o}}}{5} = {108^o}\).

Do đó, \(\widehat {EAB} = \widehat {ABC} = {108^o}\).

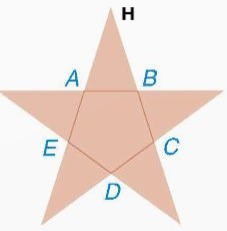
Suy ra: \(\widehat {HAB} = \widehat {HBA} = {180^o} - {108^o} = {72^o}\).

Tam giác HAB có:

\(\widehat {AHB} = {180^o} - \widehat {HAB} - \widehat {HBA} = {180^o} - {72^o} - {72^o} = {36^o}\)

Do đó, góc tạo bởi lưỡi kéo và nếp gấp lúc đầu là:

\(\frac{1}{2}\widehat {AHB} = \frac{1}{2}{.36^o} = {18^o}\).