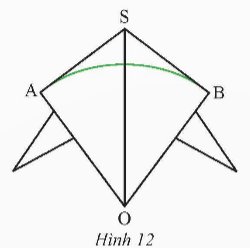
Bạn Hùng làm một cái diều với thân diều là hình tứ giác S.AOB sao cho OS là đường phân giác của \(\widehat {AOB}\) và \(\widehat {ASB} = {106^o}\). Thanh tre màu xanh lá được uốn cong thành cung AB của đường tròn tâm O và SA, SB là hai tiếp tuyến của (O) (Hình 12). Tính số đo của \(\overset\frown{AB}\).
Ta có SA, SB là hai tiếp tuyến của (O) nên OA \( \bot \) SA hay \(\widehat {OAS} = {90^o}\) và OB \( \bot \) SB hay \(\widehat {OBS} = {90^o}\).
Xét tứ giác SAOB có \(\widehat {ASB} + \widehat {OAS} + \widehat {AOB} + \widehat {OSB} = {360^o}\)
Suy ra \(\widehat {AOB} = {360^o} - \widehat {ASB} - \widehat {OAS} - \widehat {OSB} = {360^o} - {106^o} - {90^o} - {90^o} = {74^o}\)
Ta có sđ\(\overset\frown{AB}\) bị chắn bởi góc ở tâm \(\widehat {AOB}\) có số đo bằng 74o suy ra sđ\(\overset\frown{AB}\) = 74o .


