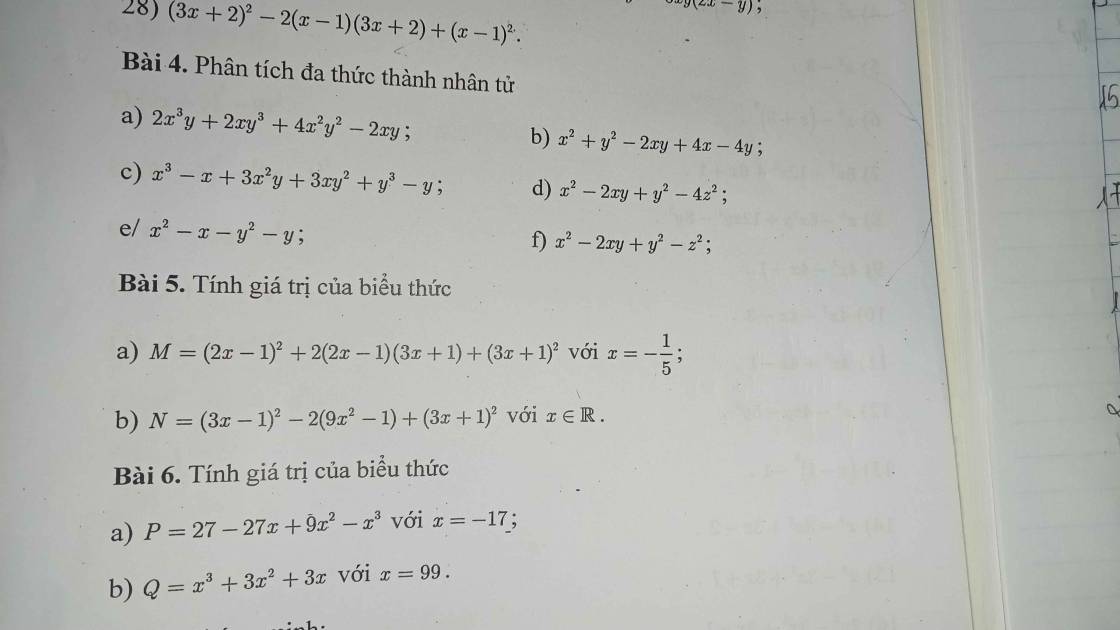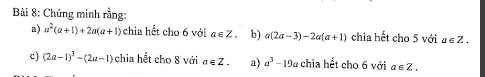Bài 5:
a) \(M=\left(2x-1\right)^2+2\left(2x-1\right)\left(3x+1\right)+\left(3x+1\right)^2\)
\(M=\left[\left(2x-1\right)+\left(3x+1\right)\right]^2\)
\(M=\left(5x\right)^2\)
Thay \(x=-\dfrac{1}{5}\) vào biểu thức M ta có:
\(\left(5\cdot-\dfrac{1}{5}\right)^2=\left(-1\right)^2=1\)
Vậy: ...
b) \(N=\left(3x-1\right)^2-2\left(9x^2-1\right)+\left(3x+1\right)^2\)
\(N=\left(3x-1\right)^2-2\left(3x+1\right)\left(3x-1\right)+\left(3x+1\right)^2\)
\(N=\left[\left(3x-1\right)-\left(3x+1\right)\right]^2\)
\(N=\left(-2\right)^2=4\)
Vậy: ...
4
a
\(=2xy\left(x^2+y^2+2xy-1\right)=2xy\left[\left(x+y\right)^2-1^2\right]\\ =2xy\left(x+y-1\right)\left(x+y+1\right)\)
b
\(=\left(x-y\right)^2+4\left(x-y\right)=\left(x-y\right)\left(x-y+4\right)\)
c
\(=\left(x+y\right)^3-\left(x+y\right)\\ =\left(x+y\right)\left[\left(x+y\right)^2-1\right]=\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\)
d
\(=\left(x-y\right)^2-\left(2z\right)^2=\left(x-y-2z\right)\left(x-y+2z\right)\)
e
\(=\left(x-y\right)\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(x-y-1\right)\)
f
\(=\left(x-y\right)^2-z^2=\left(x-y-z\right)\left(x-y+z\right)\)