Question

bài 31,35 SGK toán hình lớp 7 trang120,123

Answer 1

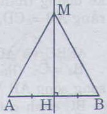
Bài 31: Đề bài: CHo đoạn AB, điểm nằm trên đường trung trực của AB. SO sánh độ dài đoạn thẳng MA và MB.

Đường trung trực của AB có chứa điểm M, cắt AB tại H

=> AH = HB

Vì a là đường trung trực của AB

=> \(a\perp AB\) và \(MHB=MHA=90^{\sigma}\)

Xét \(\Delta AMH\) và \(\Delta HMB:\)

MH : Cạnh chung (gt)

MHA = MHB

HA = HB

DO đó: \(\Delta MHA=\Delta MHB\left(c.g.c\right)\)

=> MA = MB ( 2 cạnh tương ứng )

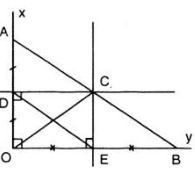
Bài 35: Cho góc xOy khác góc bẹt, Ot là tia phân giác của góc đó. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot, nó cắt Ox và Oy tnel thứ tự ở A và B

a, Chứng minh OA = OB

b, Lấy điểm C thuộc tia Ot, chứng minh rằng CA = Cb và góc OAC = góc OBC.

Giải

Vì Ot là tia phân giác của xOy

=> yOt = xOt = xOy : 2

hay BOH = AOH = xOy : 2

Xét \(\Delta BOH\) và \(\Delta AOH:\)

BOH = AOH ( chứng minh trên )

OH : cạnh chung (gt)

OHA = OHB ( = 90* )

Do đó \(\Delta BOH=\Delta AOH\left(g.c.g\right)\)

=> OA = OB ( 2 cạnh tương ứng ) đpcm

b, Xét \(\Delta BCO,\Delta ACO:\)

OC : cạnh chung (gt)

BOC = AOC

OA = OB ( câu a )

Do đó \(\Delta BCO=\Delta ACO\left(c.g.c\right)\)

=> ACO = BCO ( 2 góc tương ứng )

và OAC = OBC ( 2 góc tương ứng ) đpcm

Vì BCH + BCO = 180* ( 2 góc kề bù )

ACO + ACH = 180* ( 2 góc kề bù )

mà ACO = BCO ( chứng minh trên )

=> BCH = ACH

Xét \(\Delta BCH,\Delta ACH:\)

CH: cạnh chung (gt)

BCH = ACH ( chứng minh trên )

CHA = CHB ( =90* )

Do đó \(\Delta BCH=\Delta ACH\) ( cạnh huyền - góc nhọn )

=> CA = CB ( 2 cạnh tương ứng ) đpcm

Answer 2

Bài 31. Cho độ dài đoạn thẳng AB, điểm nằm trên đường trung trực của AB, so sánh độ dài các đoạn MA,MB.

Giải:

Goi H là trung giao điểm của đường trung trực với đoạn AB,∆AHM=∆BHM(c .g.c )

Vậy MA= MB(hai cạnh tương ứng).

 

Bài 35. Cho góc xOy khác góc bẹt, Ot là tia phân giác của góc đó. Qua H thuộc tia Ot , kẻ đường vuông góc với Ot, nó cắt Ox và Oy theo thứ tự A và B.

a) Chứng minh rằng OA=OB.

b ) Lấy điểm C thuộc tia Ot, chứng minh rằng CA=CB và = .

Giải

a) ∆AOH và ∆BOH có:=(gt)

OH là cạnh chung

∆AOH =∆BOH( g.c.g)

Vậy OA=OB.

b) ∆AOC và ∆BOC có:

OA=OB(cmt)

=(gt)

OC cạnh chung.

Nên ∆AOC= ∆BOC(g.c.g)

Suy ra: CA=CB(cạnh tương ứng)

= ( góc tương ứng).