Question

Bài 3: Cho nửa đường tròn (O) đường kính AB và AC là một dây của nó. Kẻ tiếp tuyến Ax và kẻ đường phân giác của góc CAx cắt nửa đường tròn tại E và cắt BC kéo dài tại D. a/C/m: AABD cân. b/ C/m: OE // BD. c/Gọi I là giao điểm của AC và BE. C/m: DI ⊥ AB. d/Tính độ dài AE, biết AB = 2cm và BAC = 20°,

Answer 1

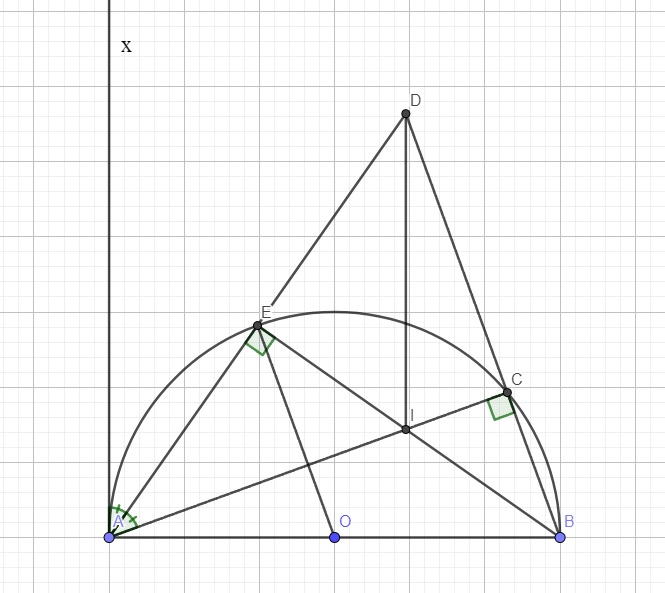
a.

Do \(\widehat{ACB}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ACB}=90^0\)

\(\Rightarrow\widehat{ACD}=90^0\Rightarrow\Delta ACD\) vuông tại C

\(\Rightarrow\widehat{ADC}+\widehat{DAC}=90^0\) (1)

Lại có \(\widehat{DAC}=\widehat{DAx}\) (do AD là phân giác)

\(\widehat{BAE}+\widehat{DAx}=90^0\) (Ax là tiếp tuyến tại A)

\(\Rightarrow\widehat{BAE}+\widehat{DAC}=90^0\) (2)

(1);(2) \(\Rightarrow\widehat{ADC}=\widehat{BAE}\)

\(\Rightarrow\Delta ABD\) cân tại B

b.

\(\widehat{AEB}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{AEB}=90^0\Rightarrow AE\perp BE\)

\(\Rightarrow BE\) là đường cao trong tam giác BAD

Mà tam giác BAD cân tại B \(\Rightarrow BE\) đồng thời là trung tuyến

\(\Rightarrow E\) là trung điểm AD

Lại có O là trung điểm AB

\(\Rightarrow OE\) là đường trung bình tam giác ABD

\(\Rightarrow OE||BD\)

Answer 2

c.

Xét tam giác ABD có: \(AC\perp BD;BE\perp AD\)

\(\Rightarrow I\) là trực tâm tam giác ABD

\(\Rightarrow DI\) là đường cao thứ 3

\(\Rightarrow DI\perp AB\)

d.

Ta có: \(\widehat{BAC}+\widehat{CAx}=90^0\)

\(\Rightarrow\widehat{BAC}+2.\widehat{CAE}=90^0\)

\(\Rightarrow\widehat{CAE}=\dfrac{90^0-20^0}{2}=35^0\)

\(\Rightarrow\widehat{BAE}=\widehat{BAC}+\widehat{CAE}=20^0+35^0=55^0\)

Xét tam giác vuông ABE có:

\(cos\widehat{BAE}=\dfrac{AE}{AB}\Rightarrow AE=AB.cos\widehat{BAE}=2.cos55^0\approx1,15\left(cm\right)\)

Answer 3