\(K=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{1}{a-\sqrt{a}}\right):\left(\dfrac{1}{\sqrt{a}+1}+\dfrac{2}{a-1}\right)\)
Đk: \(a\ge0\) và \(a\ne1\)
\(=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\left(\dfrac{1}{\sqrt{a}+1}+\dfrac{2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\right)\)
\(=\left(\dfrac{a-1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\left(\dfrac{\sqrt{a}-1+2}{(\sqrt{a}+1)\left(\sqrt{a}-1\right)}\right)\)
\(=\dfrac{a-1}{\sqrt{a}\cdot\left(\sqrt{a}-1\right)}\cdot\dfrac{\sqrt{a+1}\cdot\sqrt{a-1}}{\sqrt{a}+1}=\dfrac{a-1}{\sqrt{a}}\)
\(K=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{1}{a-\sqrt{a}}\right):\left(\dfrac{1}{\sqrt{a}+1}+\dfrac{2}{a-1}\right)\\ =\left(\dfrac{\sqrt{a}}{\sqrt{â}-1}-\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\left(\dfrac{1}{\sqrt{a}+1}+\dfrac{2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\right)\\ =\left(\dfrac{a-1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\left(\dfrac{\sqrt{a}-1+2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\right)\\ =\dfrac{a-1}{\sqrt{a}\left(\sqrt{a}-1\right)}.\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\\ =\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}}.\dfrac{\sqrt{a}+1}{\sqrt{a}+1}=\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}}=\dfrac{a-1}{\sqrt{a}}\)
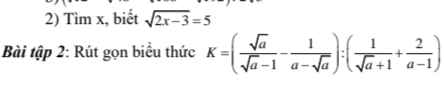
Giải giúp bài 1 2 3 4 của bài 15 i
