bài 48
Hình dưới cho biết ˆA=140∘;ˆB=70∘;ˆC=150∘A^=140∘;B^=70∘;C^=150∘
Chứng minh rằng Ax // Cy
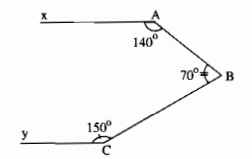
Giải
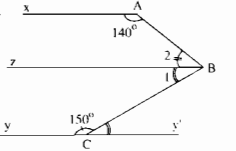
Kẻ tia Bz // Ax và Cy’ là tia đối của tia Cy
Ta có: ˆB2+ˆxAB=180∘B2^+xAB^=180∘ (hai góc trong cùng phía)
Mà ˆxAB=140∘(gt)xAB^=140∘(gt)
Suy ra: ˆB2=180∘−ˆxABB2^=180∘−xAB^
⇒⇒ ˆB2=180∘−140∘=40∘B2^=180∘−140∘=40∘
Mà ˆB1+ˆB2=ˆABCB1^+B2^=ABC^
⇒ˆB1=ˆABC−ˆB2⇒B1^=ABC^−B2^
= 70° - 40° = 30° (1)
ˆyCB+ˆBCy′=180∘yCB^+BCy′^=180∘ (2 góc kề bù)
⇒ˆBCy′=180∘−ˆyCB=180∘−150∘=30∘(2)⇒BCy′^=180∘−yCB^=180∘−150∘=30∘(2)
Từ (1) và (2) suy ra: ˆB1=ˆBCy′B1^=BCy′^
Suy ra: Cy’ // Bz (Vì có cặp góc ở vị trí so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra l ; Ax // Cy
bài 49
Hình dưới cho biết ˆA=140∘;ˆB=70∘;ˆC=150∘A^=140∘;B^=70∘;C^=150∘
Chứng minh rằng Ax // Cy

Giải

Kẻ tia Bz // Ax và Cy’ là tia đối của tia Cy
Ta có: ˆB2+ˆxAB=180∘B2^+xAB^=180∘ (hai góc trong cùng phía)
Mà ˆxAB=140∘(gt)xAB^=140∘(gt)
Suy ra: ˆB2=180∘−ˆxABB2^=180∘−xAB^
⇒⇒ ˆB2=180∘−140∘=40∘B2^=180∘−140∘=40∘
Mà ˆB1+ˆB2=ˆABCB1^+B2^=ABC^
⇒ˆB1=ˆABC−ˆB2⇒B1^=ABC^−B2^
= 70° - 40° = 30° (1)
ˆyCB+ˆBCy′=180∘yCB^+BCy′^=180∘ (2 góc kề bù)
⇒ˆBCy′=180∘−ˆyCB=180∘−150∘=30∘(2)⇒BCy′^=180∘−yCB^=180∘−150∘=30∘(2)
Từ (1) và (2) suy ra: ˆB1=ˆBCy′B1^=BCy′^
Suy ra: Cy’ // Bz (Vì có cặp góc ở vị trí so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra l ; Ax // Cy
Bn viết đề ra đi mik giải cho. mình ko có sách lớp 6
Cam on tat ca nhung ng da quan tam den bcau hoi cua mk!![]()










