Ai làm đc hok??
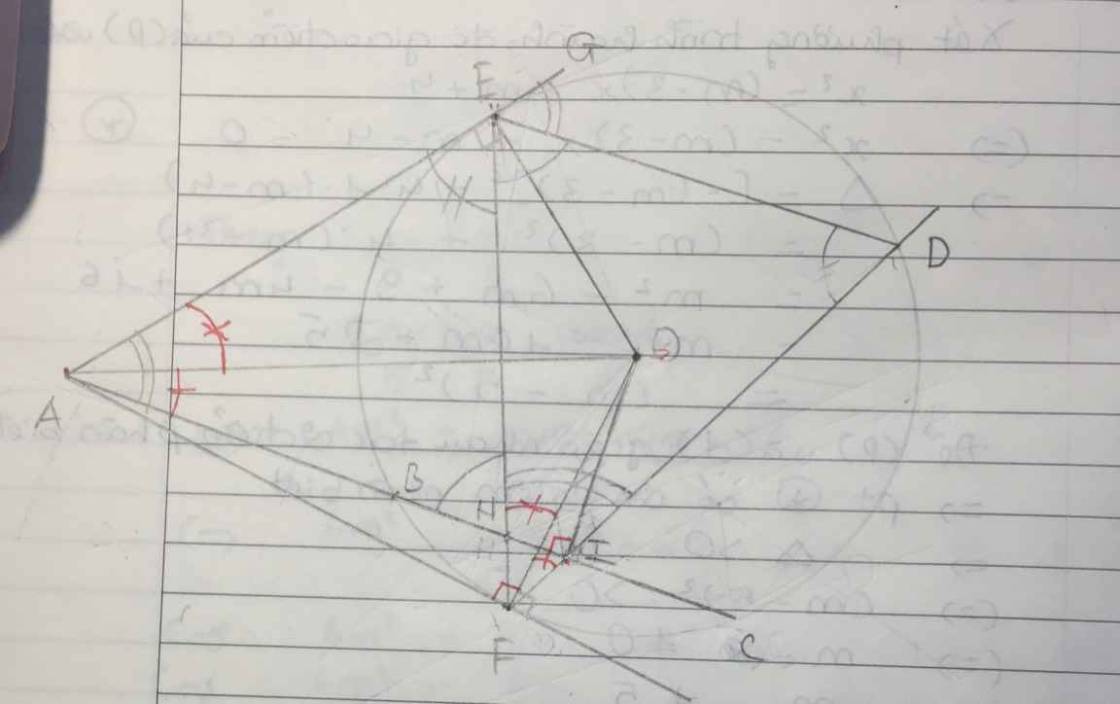
Cho điểm A cố định nằm ngoài đường tròn \(\left(O\right)\). Kẻ các tiếp tuyến AE,AF với \(\left(O\right)\) (E F là các tiếp điểm). Điểm D di động trên cung lớn EF sao cho tam giác DEF nhọn. Tiếp tuyến tại D của \(\left(O\right)\) cắt các tia AE AF lần lượt tại B,C. Gọi M, N lần lượt là giao điểm của đường thẳng EF với các đường thẳng OB,OC.
a) Chứng minh bốn điểm B,M,N,C cùng thuộc một đường tròn.
b) Gọi DK,OI lần lượt là đường phân giác của \(\widehat{EDF};\widehat{BOC}\left(K\in EF;I\in BC\right)\). Chứng minh đường thẳng IK luôn đi qua một điểm cố định
a) có CNF + NFD=90
MBC+EFD=90
=> MBC+EFD=90
=>MBC=MNC
=> TG BNMC nội tiếp (đpcm)