Tham khảo:
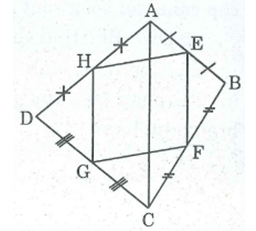
Nối đường chéo AC.
Trong ΔABC ta có:
E là trung điểm của AB (gt)
F là trung điểm của BC (gt)
Nên EF là đường trung bình của ΔABC
⇒EF//AC và EF = 1/2 AC
(tính chất đường trung hình tam giác) (1)
Trong ΔADC ta có:
H là trung điểm của AD (gt)
G là trung điểm của DC (gt)
Nên HG là đường trung bình của ΔADC
⇒ HG // AC và HG = 1/2 AC (tính chất đường trung bình tam giác) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Vậy tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
Mượn ảnh, lười vẽ:
Xét ΔABC có:
AE = EB (gt)
BF = CF (gt)
=> EF là đường trung bình của ΔABC
=> EF || AC, EF = AC (1)
C/m tương tự: ΔACD có:
HG là đường trung bình của ΔACD
=> HG || AC, HG = AC (2)
Từ (1), (2) => EF || HE và EF = HE
=> EFGH là hình bình hành










 guoi
guoi









